1. Математика
  2. Найти общее решение дифференциального

Найти общее решение дифференциального уравнения второго порядка
15y′′+11y′+2y=0

seterkton seterkton    1   21.07.2021 19:54    0

Ответы
linabananchik linabananchik  21.07.2021 20:00

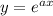Пусть y=e^{ax}. Получим соответствующее характеристическое уравнение.

15a^2+11a+2=0

D=11^2-4*15*2=121-120=1

x_1=\dfrac{-11+1}{2\cdot15}=-\dfrac{10}{30}=-\dfrac{1}{3}

x_2=\dfrac{-11-1}{2\cdot15}=-\dfrac{12}{30}=-\dfrac{2}{5}

Выполнив обратную замену, найдём общее решение соответствующего дифференциального уравнения

y=C_1e^{-x/3}+C_2e^{-2x/5}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
rickieee rickieee  09.06.2019 02:00
Решите неравенство 100^2х+1 0,1...
Senn7 Senn7  09.06.2019 02:00
Выполните действия: 2 1/3*9/14-5: 3 4/7...
Dragolord Dragolord  09.06.2019 02:00
Впервый день медицинский осмотр в школе всех шестиклассников.во второй -20 шестиклассников,которые составили 4/5 числа учеников осмотр в первый день.сколько шестиклассников...
ВикаГросс ВикаГросс  09.06.2019 02:00
Выражение : cos(п-а) -cos(-a)и найдите его значение при а=п/4...
asura3 asura3  09.06.2019 02:00
Решить систему уравнений сложения)...
приветпрррррр20246р приветпрррррр20246р  09.06.2019 02:00
Решите виленкина 6 класс (а) -2/3*3/8 б) 4/15 *(-12/25) в) -5/9 *(-12/25) г) -3 1/2 *(-4/7) д) 1 1/8 *(-5 1/3 ) е) -3 3/5 * 6 1/4 ж) - 3 1/5 * 1,2 з)1,8 *(- 1 1/3)...
shestukhina1973 shestukhina1973  09.06.2019 02:00
Решите виленкина 6 класс 2 2/9*3,7-2 2/9*(-5,3)...
dfoddo dfoddo  09.06.2019 02:00
Укати было 8 открыток. несколько открыток она отдала подруге, после чего у нее осталось 5 открыток. сколько открыток отдала катя подруге?...
анна2170 анна2170  09.06.2019 02:00
Цена на картофель в начале сентября понизился на 25% , а в конце октября повысился на 20%.какова стала цена в конце октября?...
gaiciuknataliaozve2o gaiciuknataliaozve2o  09.06.2019 02:00
Найдите разность арифметической прогрессии а1=7.а16=67...

Популярные вопросы