Найти общее решение дифференциального уравнения.

+ ещё одна задачка
y два штриха =-sin4x

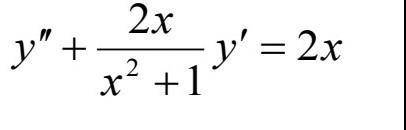
Найти общее решение дифференциального уравнения.+ ещё одна задачка y два штриха =-sin4x

Ответы

Алёнажж 29.04.2021 10:19

Первое уравнение - это ДУ 2го порядка, решающееся понижением порядка (далее, после замены, линейное ДУ)

$y'' + \frac{2x}{1 + {x}^{2} } y' = 2x \\$

$y '= z(x) \\ y'' = z'(x)$

$z '+ \frac{2x}{1 + {x}^{2} } z = 2x \\$

линейное ДУ

$z = uv \\ z' = u'v + v'u$

$u'v + v'u + \frac{2x}{1 + {x}^{2} } uv = 2x \\ u'v + u(v '+ \frac{2xv}{1 + {x}^{2} } ) = 2x \\ \\ 1)v '+ \frac{2xv}{1 + {x}^{2} } = 0 \\ \frac{dv}{dx} = - \frac{2xv}{1 + {x}^{2} } \\ \int\limits \frac{dv}{v} = - \int\limits \frac{2x}{1 + {x}^{2} } dx \\ ln(v) = - \int\limits \frac{d(1 + {x}^{2}) }{1 + {x}^{2} } \\ ln(v) = - ln(1 + {x}^{2} ) \\ v = \frac{1}{1 + {x}^{2} } \\ \\ 2)u'v = 2x \\ \frac{du}{dx} \times \frac{1}{1 + {x}^{2} } = 2x \\ \int\limits \: du = \int\limits2x(1 + {x}^{2}) dx \\ u = \int\limits(2x + 2 {x}^{3} )dx = \frac{2 {x}^{2} }{2} + \frac{2 {x}^{4} }{4} + C_1 = \\ = {x}^{2} + \frac{ {x}^{4} }{2} + C_1 \\ z = uv = \frac{1}{1 + {x}^{2} } ( {x}^{2} + \frac{ {x}^{4} }{2} + C_1) \\ z = \frac{2 {x}^{2} + {x}^{4} + 2C_1 }{1 + {x}^{2} } \\ \\ y = \frac{ {x}^{4} + 2 {x}^{2} + C_1 }{1 + {x}^{2} } \\ y = \int\limits \frac{ {x}^{4} + 2 {x}^{2} + C_1 }{1 + {x}^{2} } dx = \\ = \int\limits \frac{ {x}^{4} + 2 {x}^{2} }{1 + {x}^{2} } dx + \int\limits \frac{C_1dx}{1 + {x}^{2} }$

в первом интеграле разделим числитель на знаменатель:

$y = \int\limits( {x}^{2} + 1 - \frac{1}{1 + {x}^{2} } )dx + \int\limits \frac{C_1dx}{1 + {x}^{2} } = \\ = \frac{ {x}^{3} }{3} + x - arctgx + C_1arctgx + C_2 = \\ = \frac{ {x}^{3} }{3} + x + C_1arctgx + C_2$

общее решение

ДУ 2го порядка, решающееся интегрированием

$y''= - \sin(4x) \\ y'= - \int\limits \sin(4x) dx = - \frac{1}{4} \int\limits \sin(4x) d(4x) = \\ = \frac{1}{4} \cos(4x) + C_1 \\ y = \int\limits( \frac{1}{4} \cos(4x) + C_1)dx = \\ = \frac{1}{4} \times \frac{1}{4} \int\limits \cos(4x) d(4x) + C_1x + C_2 = \\ = \frac{1}{16} \sin(4x) + C_1x + C_2$