Найти общее решение дифференциального уравнения
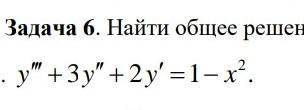
Другие вопросы по теме Математика
Популярные вопросы
- 25 1. столица византии (город константинополь) располагалась на берегу пролива...
3 - Отношение пушкина к марии гавриловне повесть метель...
2 - Ззагадки на ійській мові про професії...
3 - Преимущества электронной книги над печатной 2. ,,преимущества печатней книги...
1 - Длина отрезка ав равна 12 см. сколько существует на прямой ав точек для которых...
2 - Почему город мехико ежегодно затапливается...
3 - Здесь есть кто-то кто разбирается в тех механике?...
2 - Пять предложений нашему поздняя осень где сказуемое прилагательным...
1 - Отметьте случаи лексической несочетаемости слов. 1. проявить желание, проявить...
3 - Запишите в виде десятичной дроби 1/2 4/25 7/8 11/125...
1
ответ: y=C1*e^(-x)+C2*e^(-2*x)+C3-1/6*x³+3/4*x²-7/4*x.
Пошаговое объяснение:
Так как данное уравнение не содержит искомой функции y, то его порядок можно снизить на 1. Полагаем y'=z, тогда уравнение принимает вид: z"+3*z'+2*z=1-x². Перед нами - неоднородное ЛДУ 2 порядка с постоянными коэффициентами и с правой частью "специального" вида f(x)=e^(m*x)*[P1(x)*cos(n*x)+P2(x)*sin(n*x)], где m=n=0, P1(x)=1-x², P2(x)=0. Соответствующее однородное ДУ имеет вид: z"+3*z'+2*z=0. Для его решения составляем характеристическое уравнение (ХУ): k²+3*k+2=0. Оно имеет корни k1=-1 и k2=-2, поэтому общее решение z1 однородного уравнения таково: z1=A1*e^(-x)+A2*e^(-2*x), где A1 и A2 - произвольные постоянные. Переходим теперь к нахождению частного решения z2 данного неоднородного уравнения. так как числа m+i*n=0 и m-i*n=0 не являются корнями ХУ, то z2=e^(m*x)*[R1(x)*cos(n*x)+R2(x)*sin(n*x)]=P1(x), где R1(x) - многочлен, степень которого равна старшей степени многочленов P1(x) и P2(x). Так как эта старшая степень равна 2, то P1(x)=a*x²+b*x+c, где a, b, c - неизвестные пока коэффициенты. Дважды дифференцируя z2, подставляя выражения для z2, z2' и z2" в уравнение и приводя подобные члены, приходим к уравнению: 2*a*x²+x*(6*a+2*b)+(3*b+2*c)=-x²+1. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений:
2*a=-1
6*a+2*b=0
3*b+2*c=1
Решая её, находим a=-1/2, b=3/2, c=-7/4. Отсюда z2=-1/2*x²+3/2*x-7/4 и тогда общее решение уравнения z=y'=A1*e^(-x)+A2*e^(-2*x)-1/2*x²+3/2*x-7/4. Интегрируя, находим
y=-A1*e^(-x)-1/2*A2*e^(-2*x)-1/6*x³+3/4*x²-7/4*x+C3, где C3 - произвольная постоянная. Полагая C1=-A1 и C2=-1/2*A2, получаем: y=C1*e^(-x)+C2*e^(-2*x)-1/6*x³+3/4*x²-7/4*x+C3.