Найти область сходимости степенного ряда
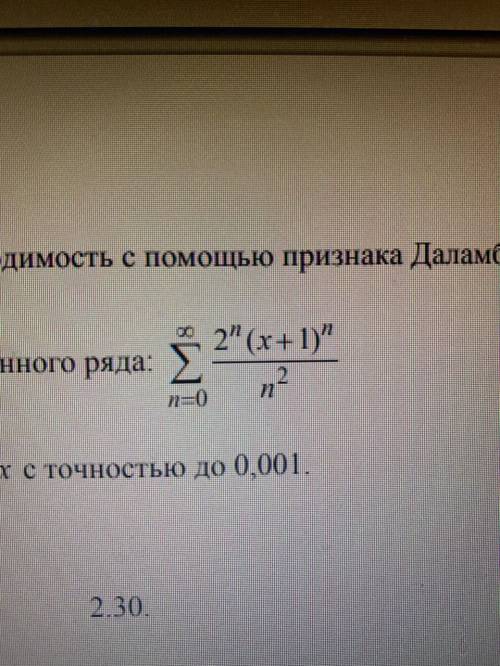
Другие вопросы по теме Математика
Популярные вопросы
- Решите уравнение 144 -x в квадрате =0 169...
3 - Две фабрики выпускают одинаковые стекла для автомобильных фар. первая фабрика выпускает...
2 - 98 ! надо составить диалог на основе этого текста на казахском языке: байқоңыр-12...
3 - Представьте в виде обыкновенной несократимой дроби: 0,2; 0,8; 0,5; 0,24; 0,35; 0,75;...
3 - Как в столбик делать умножение двухзначных чисел? ответ с объяснением 33 ...
3 - На с#, 1. определить, является ли число а делителем числа b ...
2 - Просклонять мечта, ночь, апельсин в ед.ч и к каждому из слов подобрать по 2однакорекнног...
1 - Ажетті сөздермен толықтырып жаз. ақ,қара,үлкен...
2 - Напишите 5 предложений с фразеологизмами но что бы в них были деепричастия...
3 - Взяли для очистки 12,5 кг моркови. отходы при холодной обработке 20% от веса брутто....
2
Введу некоторые поправки: сумма начинается с n = 1.
Степенной ряд в общем виде записывается следующим образом: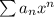 , где
, где 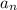 - формула числовых коэффициентов. Для данного ряда:
- формула числовых коэффициентов. Для данного ряда: 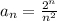 . Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
. Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу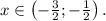 Теперь нужно проверить сходимость ряда на концах этого интервала.
Теперь нужно проверить сходимость ряда на концах этого интервала.
Если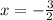 имеем
имеем 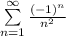 - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
- числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется. Таким образом, предложенный рассматриваемый ряд сходится. Теперь нужно проверить на условной и абсолютной сходимости ряда. Возьмём ряд по модулю: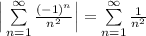 - сходящийся ряд. Следовательно, ряд
- сходящийся ряд. Следовательно, ряд 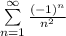 сходится абсолютно, значит
сходится абсолютно, значит 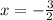 — точка сходимости.
— точка сходимости.
Аналогично, если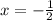 , имеем
, имеем 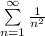 — сходящийся ряд. Следовательно,
— сходящийся ряд. Следовательно,
Таким образом, данный степенной ряд является сходящимся при![x \in [-\frac{3}{2};-\frac{1}{2}].](/tpl/images/1356/8046/1421e.png)