Найти объем тела, ограниченного поверхностями: z = 4 - x^2, 2x + y = 4, x = 0, y = 0, z = 0 (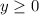 )
)
Другие вопросы по теме Математика
Популярные вопросы
- Розгляньте малюнок і поясніть , де алегорія?...
3 - Как вы думаете, каково будущее цифровых технологий?...
3 - В стаде было 300 животных, из них 36% составляют овцы. Сколько овец было в стаде?...
2 - Михаил иванович глинка попутная песня какой темп в музыке...
1 - Постановка толчковой ноги (по отношению к планки) является типичной ошибкой...
3 - Развернутый ответ Жан Кальвин и его вклад в рас реформации.Сррчно...
1 - Произведите синтаксический разбор предложений. Обсудив положение, мы решили...
3 - Какие группы мышц участвуют в броске одной рукой в баскетболе? ответить кратко....
2 - Знайдіть 5-й член геометричної прогресії (аn), якщо а1=17, d=4.а)33; б)-33;...
3 - «Век живи – век люби» В.Г. Распутина 5-6 во к ему рассказу...
2
В данном случае, у нас есть следующие поверхности: z = 4 - x^2, 2x + y = 4, x = 0, y = 0, z = 0 и ограничение y ≥ 0.
Для начала, давайте построим графики предоставленных уравнений.
Уравнение z = 4 - x^2 представляет собой параболу, которая открывается вниз и с вершиной в точке (0, 4). Обратите внимание, что данное уравнение имеет ограничение на переменные z и x: оно будет лежать только в области, где z ≥ 0.
Уравнение 2x + y = 4 представляет собой прямую линию с угловым коэффициентом 2 и точкой пересечения с осью y в точке (0, 4). Также обратите внимание, что данное уравнение имеет ограничение на переменную y: она должна быть больше или равна нулю.
Теперь, вам нужно найти область пересечения между этими двумя поверхностями. Для этого воспользуемся системой уравнений, состоящей из обоих уравнений.
Система уравнений будет выглядеть следующим образом:
1) z = 4 - x^2
2) 2x + y = 4
Давайте решим эту систему уравнений методом подстановки.
Сначала выразим переменную y из второго уравнения:
y = 4 - 2x
Теперь подставим это значение y в первое уравнение:
z = 4 - x^2
Таким образом, мы получили новое уравнение:
z = 4 - x^2
Мы можем видеть, что данное уравнение описывает тот же график, что и первое уравнение z = 4 - x^2. Это означает, что область пересечения между двумя поверхностями представляет собой параболу, которая открывается вниз и с вершиной в точке (0, 4).
Теперь, чтобы найти объем тела, ограниченного этими поверхностями, вам нужно провести интегрирование этого графика по оси z на интервале, где z ≥ 0.
Для этого, мы будем использовать формулу для вычисления объема трехмерной фигуры:
V = ∫∫∫ dV
где dV - это объемный элемент, который представляет собой маленький объем внутри фигуры.
В данном случае, dV будет представлять собой dx dy dz, так как наши поверхности заданы в терминах x, y и z переменных.
Теперь, давайте проинтегрируем наше уравнение по оси z на интервале, где z ≥ 0.
V = ∫∫∫ dz dy dx
Заметим, что наши пределы интегрирования по z будут от нуля до 4 - x^2, по y будут от нуля до 4 - 2x, а по x будут от нуля до 2.
V = ∫(0 to 2) ∫(0 to 4 - 2x) ∫(0 to 4 - x^2) dz dy dx
Теперь давайте проинтегрируем это выражение по z, используя полученные пределы интегрирования.
V = ∫(0 to 2) ∫(0 to 4 - 2x) (4 - x^2) dy dx
Теперь, проинтегрируем это по y.
V = ∫(0 to 2) [(4 - x^2)(4 - 2x)] dx
Теперь, проинтегрируйте это выражение по x.
V = ∫(0 to 2) [8x - 4x^2 - 2x^3 + x^4] dx
Вычислим этот интеграл:
V = [4x^2 - (4/3)x^3 - (1/2)x^4 + (1/5)x^5] с 0 до 2
V = [4(2)^2 - (4/3)(2)^3 - (1/2)(2)^4 + (1/5)(2)^5] - [4(0)^2 - (4/3)(0)^3 - (1/2)(0)^4 + (1/5)(0)^5]
V = [16 - (32/3) - 8 + 32/5] - [0]
V = [80/15 - 160/15 - 120/15 + 96/15]
V = -104/15
Таким образом, объем тела, ограниченного данными поверхностями, равен -104/15.