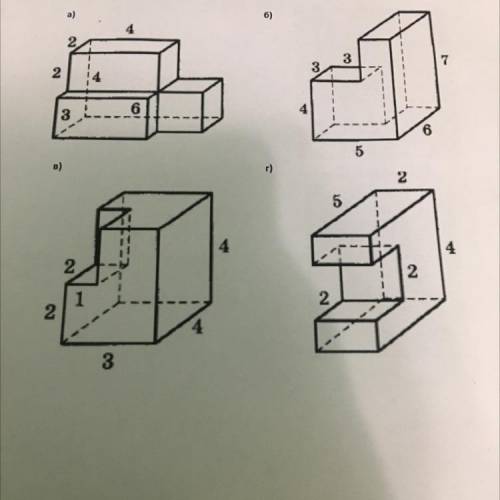
Найти объем и площадь поверхности четырех фигур

Добрый день! С удовольствием помогу вам решить эту задачу.

Первая фигура - это прямоугольный параллелепипед. Чтобы найти его объем, нужно перемножить длину, ширину и высоту. Даны следующие данные: длина = 10 см, ширина = 5 см, высота = 3 см.

Объем прямоугольного параллелепипеда рассчитывается по формуле V = длина * ширина * высота. Вставим значения в формулу:

V = 10 см * 5 см * 3 см = 150 см³.

Ответ: объем прямоугольного параллелепипеда равен 150 см³.

Чтобы найти площадь поверхности прямоугольного параллелепипеда, нужно посчитать площади всех его граней и сложить их.

У прямоугольного параллелепипеда шесть граней: две большие грани, которые являются прямоугольниками, и четыре боковые грани, которые являются прямоугольниками.

Чтобы найти площадь каждой грани, нужно перемножить длину и ширину. Затем нужно сложить площади всех граней.

Даны следующие данные: длина = 10 см, ширина = 5 см, высота = 3 см.

Площадь грани, являющейся прямоугольником, рассчитывается по формуле S = длина * ширина. Вставим значения в формулу:

Площадь одной большой грани: S1 = 10 см * 5 см = 50 см².
Площадь одной боковой грани: S2 = 10 см * 3 см = 30 см².

Так как прямоугольный параллелепипед имеет две большие грани и четыре боковые грани, общая площадь поверхности будет равна:

Sобщ = 2 * S1 + 4 * S2 = 2 * 50 см² + 4 * 30 см² = 100 см² + 120 см² = 220 см².

Ответ: площадь поверхности прямоугольного параллелепипеда равна 220 см².

Вторая фигура - это прямая призма. Чтобы найти ее объем, нужно перемножить площадь основания и высоту. Даны следующие данные: площадь основания = 40 см², высота = 8 см.

Объем прямой призмы рассчитывается по формуле V = площадь основания * высота. Вставим значения в формулу:

V = 40 см² * 8 см = 320 см³.

Ответ: объем прямой призмы равен 320 см³.

Чтобы найти площадь поверхности прямой призмы, нужно сложить площади всех ее граней.

У прямой призмы три грани: две основных, которые являются одинаковыми копиями друг друга, и одну боковую.

Площадь основания уже известна: S1 = 40 см².
Площадь боковой грани равна периметру основания, умноженному на высоту. Периметр основания можно найти, просуммировав все стороны основания.

Даны следующие данные о сторонах основания: AB = 4,5 см, BC = 4,5 см, CD = 4 см, DA = 4 см.

Периметр основания: P = AB + BC + CD + DA = 4,5 см + 4,5 см + 4 см + 4 см = 17 см.

Площадь боковой грани: S2 = P * высота = 17 см * 8 см = 136 см².

Так как у прямой призмы две основные грани и одна боковая грань, общая площадь поверхности будет равна:

Sобщ = 2 * S1 + S2 = 2 * 40 см² + 136 см² = 80 см² + 136 см² = 216 см².

Ответ: площадь поверхности прямой призмы равна 216 см².

Третья фигура - это пирамида. Чтобы найти ее объем, нужно перемножить площадь основания на высоту, а затем разделить полученное значение на 3. Даны следующие данные: площадь основания = 25 см², высота = 6 см.

Объем пирамиды рассчитывается по формуле V = (площадь основания * высота) / 3. Вставим значения в формулу:

V = (25 см² * 6 см) / 3 = 150 см³ / 3 = 50 см³.

Ответ: объем пирамиды равен 50 см³.

Чтобы найти площадь поверхности пирамиды, нужно сложить площади всех ее граней.

У пирамиды пять граней: одну основную, которая является квадратом, и четыре треугольные боковые грани.

Площадь основания уже известна: S1 = 25 см².

Площадь боковой грани, являющейся треугольником, можно найти, используя формулу Герона. Формула Герона позволяет найти площадь треугольника, используя длины его сторон.

Даны следующие данные о сторонах треугольника: AB = 4,5 см, BC = 4,5 см, AC = 3 см.

Сначала найдем полупериметр треугольника, который вычисляется по формуле P = (AB + BC + AC) / 2:

P = (4,5 см + 4,5 см + 3 см) / 2 = 12 см / 2 = 6 см.

Теперь можем использовать формулу Герона для расчета площади треугольника:

S2 = √(P * (P - AB) * (P - BC) * (P - AC)) = √(6 см * (6 см - 4,5 см) * (6 см - 4,5 см) * (6 см - 3 см)) = √(6 см * 1,5 см * 1,5 см * 3 см) = √(40,5 см³) ≈ 6,36 см².

Так как у пирамиды одна основная грань и четыре боковые грани, общая площадь поверхности будет равна:

Sобщ = S1 + 4 * S2 = 25 см² + 4 * 6,36 см² = 25 см² + 25,44 см² ≈ 50,44 см².

Ответ: площадь поверхности пирамиды примерно равна 50,44 см².

Наконец, четвертая фигура - это цилиндр. Чтобы найти его объем, нужно перемножить площадь основания на высоту. Даны следующие данные: площадь основания = 16 см², радиус основания = 2 см, высота = 10 см.

Площадь основания уже известна: S1 = 16 см².

Объем цилиндра рассчитывается по формуле V = площадь основания * высота. Вставим значения в формулу:

V = 16 см² * 10 см = 160 см³.

Ответ: объем цилиндра равен 160 см³.

Чтобы найти площадь поверхности цилиндра, нужно посчитать площадь основания и площадь боковой поверхности, а затем сложить их.

Площадь боковой поверхности цилиндра рассчитывается по формуле S2 = 2πr * высота, где π - приближенное значение числа Пи, r - радиус основания.

В данной задаче π примем равным 3,14.

S2 = 2 * 3,14 * 2 см * 10 см = 125,6 см².

Так как у цилиндра есть площадь основания и площадь боковой поверхности, общая площадь поверхности будет равна:

Sобщ = 2 * S1 + S2 = 2 * 16 см² + 125,6 см² = 32 см² + 125,6 см² = 157,6 см².

Ответ: площадь поверхности цилиндра равна 157,6 см².

Это и есть решение задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать."