Найти объëм и площадь полной поверхности правильной шестиугольной призмы, если известно, что ребро основания равно 4см, а боковое ребро равно 10 см
Другие вопросы по теме Математика
Популярные вопросы
- Революционные события в восточной европе в конце 1980-х гг 4 вопроса...
2 - Номер 5 ! ! точки м иn находятся на одинаковом расстоянии от прямой...
3 - Когда бывает больше всего воды в днепре? в какое время днепро...
2 - Оля собрала 8 горшков для растений из деталей конструктора 1 горшок...
2 - Решите, , те, которые обеденны, хотелось бы как можно быстрее,...
1 - Найти и записать отрывок текста по другим учебным дисциплинам...
1 - Сколькими из 15 присяженых заседателей можно отобрать трёх для...
3 - Решить номер 779,не игнорьте объясните пошагово))...
3 - Составьте 10 (оригинальных) предложений с обособленными и необоснованными...
3 - Якими були місто і село у 17-18 століттях 5 - 6 речень...
3
В основании правильной шестиугольной призмы с высотой 10 см лежит шестиугольник со стороной 4 см.
1) Найдем площадь полной поверхности:
S п.п. = 3а • (а√3 + 2h)
S п.п. = 3•4 • (4√3 + 2•10) =
= 12 • (4√3 + 20) = 323,138 кв.см
2) Найдем объем правильной шестиугольной призмы.
V = (h√3)•(3а²)/2
где h - высота, а - сторона равностороннего шестиугольника в основании.
V = (10√3)•(3•4²)/2 =
= 240√3 = 415,692 куб.м.
Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
У нас боковое ребро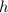 равно 10 см, а ребро основания
равно 10 см, а ребро основания  равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами
, и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами  и
и 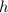 .
.
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
Где площадь основания находится согласно формуле:
А площадь боковых граней равна: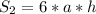
Подставляя это в формулу общей площади получим:
Подставляя наши значения получаем:
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.