1. Математика
  2. Найти неопределенный интеграл.

Найти неопределенный интеграл\int\limits Sin(5-7*x)dx. С полным решением

yliya302 yliya302    2   17.03.2021 16:26    0

Ответы
Alina22511 Alina22511  16.04.2021 16:27

\int\limits sin(5-7*x) \, dx

пусть u=5-7

Тогда du=-7dx и подставляем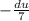 -\frac{du}{7} Получим:

\int\limits(-\frac{sin(u)}{7} \, du

Интеграл  от произведения функции на константу есть эта константа на интеграл от данной функции:

\int\limit sin(u) \, du=-\frac{\int\limits sin(u) \, du }{7}

Интеграл от синуса есть минус косинуса:

\int\limits sin(u) \, du=-cos(u)

Таким образом, результат будет: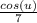\frac{cos(u)}{7} а, если сейчас заменить u еще в:

\frac{cos(7x-5)}{7}

Добавляем постоянную интегрирования;

ответ;

\frac{cos(7x-5)}{7} +constant

Либо

\frac{cos(2)}{7}-\frac{cos(5)}{7}

Пошаговое объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
незнайка1185 незнайка1185  15.07.2019 20:20
Сколько будет 233 1/3 умножить на 100...
Yasik228 Yasik228  15.07.2019 20:20
Паркетну підлогу вкрили лаком два рази. першого разу на кожний квадратний метр витратили 120 г лаку, а другого - 80 г. скільки витратили кілограмів лаку, якщо довжина...
tarantilla tarantilla  15.07.2019 20:20
Встоловой есть два вида салатов два вида первых блюд и два вида вторых. сколько вариантов выбора обедов если обед состоит из салата перваго и второго блюда...
machismo machismo  15.07.2019 20:20
Разложите на множители многочлен x в кубе плюс икс в квадрате плюс икс плюс один...
Reek5657 Reek5657  15.07.2019 20:20
По ! таблетка массой 500 мг состоит из 5 равных частей по массе частей растительного вещества 2 таких же частей вещества и 3 частей вещества какую долю таблетки...
mozgovod mozgovod  15.07.2019 20:20
2класса реши уравнения 33 - а = 90-70 17+ х =33+27 70-b=88-45...
Alisa27Alisa Alisa27Alisa  15.07.2019 20:20
2бригабды рабочих выгрузили 27 236 мешков цемента одна бригада выгрузила на 1 358 мешков цемента больше чем другая сколько мешков цементавыгрузила каждая бригада...
mi262 mi262  15.07.2019 20:20
Улитка за день заползает вверх на 2 м а сползает на 1 метр за сколько дней она доберется до верхушки...
Богдан2281667 Богдан2281667  15.07.2019 20:20
Найдите площадь круга, у которого диаметр равен 12 см. надо...
Kiki137 Kiki137  15.07.2019 20:20
Длина прямоугольника равна 10 дм, площадь -80 дм в квадрате. найди его ширину...

Популярные вопросы