Найти неопределённые интегралы методом непосредственного интегрирование а) сведением интеграл к табличному б) в) г) д) е) - пользуясь инвариантностью формулы интегрирование (подведением функции под знак дифференциала )
Результаты а) б) в) г) д) проверить путём нахождения производной от полученной функции
То что сможете решить решите хоть что-нибудь

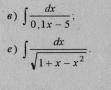
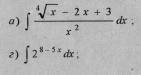
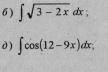
Найти неопределённые интегралы методом непосредственного интегрирование а) сведением интеграл к табл

Ответы

МАШЕНЬКА881 30.04.2021 12:33

а)

$\int {\frac{\sqrt[4]{x}-2x+3 }{x^2} } \, dx =\int {(\frac{x^\frac{1}{4}}{x^2} -\frac{2x}{x^2}+\frac{3}{x^2} )} \, dx =\int {(x^{-\frac{7}{4} } -2\cdot \frac{1}{x} +3x^{-2}}) } \, dx=\\ \\ =\frac{x^{-\frac{3}{4}}}{(-\frac{3}{4})}-2\cdot \ln{|x|}+3\cdot \frac{x^{-1}}{-1}+C=-\frac{4}{3\sqrt[4]{x^3} }-2\ln{|x|}-\frac{3}{x}+C$

$(-\frac{4}{3\sqrt[4]{x^3} }-2\ln{|x|}-\frac{3}{x}+C)'=-\frac{4}{3}\cdot (-\frac{3}{4})x^{-\frac{7}{4}}-2\cdot \frac{1}{x}-3\cdot (-1)\cdot x^{-2}=\frac{1}{x^\frac{7}{4}}-\frac{2}{x}+\frac{3}{x^2}=\\ \\ = \frac{x^\frac{1}{4}-2x+3}{x^2}= \frac{\sqrt[4]{x} -2x+3}{x^2}$

б)

$(3-2x)'=-2 \\ \\ \int {\sqrt{3-2x}} \, dx =-\frac{1}{2}\int {(3-2x)^\frac{1}{2}} \, d(3-2x)=-\frac{1}{2}\cdot \frac{(3-2x)^\frac{3}{2}}{\frac{3}{2}}=-\frac{\sqrt{(3-2x)^3} }{3}+C$

$(-\frac{\sqrt{(3-2x)^3} }{3}+C)'=-\frac{1}{3}\cdot \frac{3}{2}\cdot (3-2x)^\frac{1}{2}\cdot (3-2x)'=-\frac{1}{2}\sqrt{3-2x}\cdot (-2)=\sqrt{3-2x}$

г)

$(8-5x)'=-5 \\ \\ \int {2^{8-5x}} \, dx =-\frac{1}{5}\cdot \int {2^{8-5x}} \, d(8-5x)=-\frac{1}{5}\cdot 2^{8-5x}\cdot \frac{1}{\ln{2}}+C=-\frac{2^{8-5x}}{5\ln{2}}+C= \\ \\=-\frac{2^{8-5x}}{\ln{32}}+C$

$(-\frac{2^{8-5x}}{\ln{32}}+C)'=(-\frac{1}{\ln{32}})\cdot 2^{8-5x}\cdot \ln{2}\cdot (8-5x)'=(-\frac{1}{\ln{32}})\cdot 2^{8-5x}\cdot \ln{2}\cdot (-5)=\\ \\ = \frac{5\ln{2}}{\ln{32}}\cdot 2^{8-5x}= \frac{\ln{32}}{\ln{32}}\cdot 2^{8-5x}= 2^{8-5x}$

в)

$(0,1x-5)'=0,1\\ \\ \int {\frac{dx}{0,1x-5}}=\frac{1}{0,1}\int {\frac{d(0,1x-5)}{0,1x-5}}=10\cdot \ln{|0,1x-5|}+C \\ \\ (10\cdot \ln{|0,1x-5|}+C )'=\frac{10}{0,1x-5} \cdot (0,1x-5)'=\frac{10}{0,1x-5} \cdot 0,1 =\frac{1}{0,1x-5}$

д)

$(12-9x)'=-9\\ \\ \int {\cos{(12-9x)}} \, dx= -\frac{1}{9}\int {\cos{(12-9x)}} \, d(12-9x)=-\frac{1}{9}\cdot \sin{(12-9x)}+C$

$(-\frac{1}{9}\cdot \sin{(12-9x)}+C)'=-\frac{1}{9}\cdot \cos{(12-9x)}\cdot (12-9x)'=\\\\=-\frac{1}{9}\cdot \cos{(12-9x)}\cdot (-9)=\cos{(12-9x)}$

е)

$\int {\frac{dx}{\sqrt{1+x-x^2}}} =\int {\frac{dx}{\sqrt{-(x^2-2\cdot \frac{1}{2}\cdot x+\frac{1}{4})+\frac{5}{4}}}}= \int {\frac{dx}{\sqrt{\frac{5}{4}-(x-\frac{1}{2})^2}}} = \int {\frac{d(x-\frac{1}{2})}{\sqrt{(\sqrt{\frac{5}{4}})^2-(x-\frac{1}{2})^2}}} =\\ \\ =\arcsin{\frac{x-\frac{1}{2}}{\sqrt{\frac{5}{4}}}}+C=\arcsin{\frac{2x-1}{\sqrt{5}}}+C=\arcsin{\frac{\sqrt{5}\cdot (2x-1)}{5}}+C$

$(\arcsin{\frac{\sqrt{5}\cdot (2x-1)}{5}}+C)'=\frac{1}{\sqrt{1-(\frac{\sqrt{5}\cdot (2x-1)}{5})^2}}}\cdot (\sqrt{5}\cdot (2x-1))'=\frac{2\sqrt{5}}{\sqrt{1-\frac{4x^2-4x+1}{5}}}=\\ \\ =\frac{2}{\sqrt{5-4x^2+4x-1}}=\frac{2}{\sqrt{4-4x^2+4x}}=\frac{1}{\sqrt{1-x^2+x}}=$