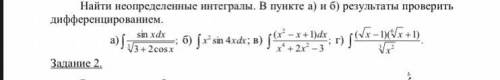
Математика: Найти неопределенные интегралы

Найти неопределенные интегралы

Ответы

vasiapasi17 28.02.2021 22:24

Пошаговое объяснение:

$\displaystyle \int {\frac{sinx}{\sqrt[3]{2cosx+3} } } \, dx =\left[\begin{array}{ccc}u=2cosx+3\\du=-2sinxdx\\\end{array}\right] =-\frac{1}{2} \int{\frac{1}{\sqrt[3]{u} } } \, du=$

$\displaystyle =-\frac{3u^{2/3}}{4} +C=-\frac{3(2cosx+3)^{3/2}}{4} +C$

б) здесь будем использовать два раза ∫fdg=fg - ∫gdf

$\int {x^2sinx} \, dx =\left[\begin{array}{ccc}f=x^2;\quad df=2xdx \hfill \\dg=sin(4x)dx;\quad g=-\frac{1}{4}cos(4x) \\\end{array}\right] =$

$\displaystyle = -\frac{1}{4} x^2cos(4x)+\frac{1}{2} \int {xcos(4x)} \, dx =\left[\begin{array}{ccc}f=x; \quad df=dx \hfill\\dg=cos(4x)dx; \quad g= \frac{1}{4}sin(4x) \\\end{array}\right] =$

$\displaystyle =-\frac{1}{4} x^2cos(4x)+\frac{1}{8} xsin(4x) -\frac{1}{8} \int {sin(4x)} \, dx =\left[\begin{array}{ccc}u=4x\\du=4dx\\\end{array}\right] =$

$\displaystyle =-\frac{1}{4} x^2cos(4x)+\frac{1}{8} xsin(4x)-\frac{1}{32} \int {sinu} \, du=$

$\displaystyle =-\frac{1}{4} x^2cos(4x)+\frac{1}{8} xsin(4x) +\frac{1}{32} cos(4x)+C$

в)

$\displaystyle \int {\frac{x^2-x+1}{x^4+2x^2-3} } \, dx$

разложим на множители знаменатель

$\displaystyle \int {\frac{x^2-x+1}{(x-1)(x+1)(x^2+3)} } \, dx$

разложим дробь на простейшие и применим линейность к интегралу

$\displaystyle =\frac{1}{4} \int {\frac{x+2}{x^2+3} } \, dx -\frac{3}{8} \int {\frac{1}{x+1} } \, dx +\frac{1}{8\int{\frac{1}{x-1} } \, dx } =$ (1)

это наш основной интеграл. сюда будем подставлять всё что будем считать по отдельности

1. считаем первый интеграл

$\displaystyle \int {\frac{x+2}{x^2+3} } \, dx =\int {\frac{x}{x^2+3} } \, dx +2\int {\frac{1}{x^2+3} } \, dx$

$\displaystyle \int {\frac{x}{x^2+3} } \, dx =\left[\begin{array}{ccc}u=x^2+3\\du=2xdx\\\end{array}\right] =\frac{1}{2} \int {\frac{1}{u} } \, du=\frac{lnu}{2} =\frac{ln(x^2+3)}{2}+C$

$\displaystyle \int {\frac{1}{x^2+3} } \, dx =\left[\begin{array}{ccc}u=x/\sqrt{3} \\dx=\sqrt{3du} \\\end{array}\right] =\frac{1}{\sqrt{3} } \int {\frac{1}{u^2+1} } \, du =\frac{arctg(u)}{\sqrt{3} } =\frac{arctg(x/\sqrt{3}) }{\sqrt{3} }++C$

вот мы получили первый интеграл

$\displaystyle \int {\frac{x+2}{x^2+3} } \, dx =\frac{ln(x^2+3)}{2} +\frac{2arctg(x/\sqrt{3}) }{\sqrt{3} }+C$

2. теперь считаем второй интеграл

$\displaystyle \int {\frac{1}{x+1} } \, dx =ln(x+1) +C$

3. теперь третий

$\displaystyle \int {\frac{1}{x-1} } \, dx =ln(x-1) +C$

ну вот и теперь всё вычисленное подставляем в интеграл (1) со всеми множителями и подставляем прямо в условие

$\displaystyle \int {\frac{x^2-x+1}{x^4+2x^2-3} } \, dx=\frac{ln(x^2+3)}{8} -\frac{3ln(x+1)}{8} +\frac{ln(x-1)}{8} +\frac{arctg(x/\sqrt{3)} }{\sqrt{3} } +C$

г) числитель перемножим и поделим каждое слагаемое на знаменатель

$\displaystyle \int {\frac{(\sqrt{x} -1)(\sqrt[6]{x}+1) }{\sqrt[3]{x^2} } } \, dx =\int{\bigg (\frac{1}{\sqrt[6]{x} }-\frac{1}{\sqrt{x} } -\frac{1}{\sqrt[3]{x^2} } +1} \bigg )\, dx =$