Найти неопределенные интегралы.
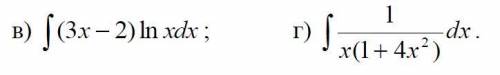
Другие вопросы по теме Математика
Популярные вопросы
- Разложите на множители многочлен х^3 -2х^2+х -2...
2 - Можите на листе сфоткать и показать решить пример столбиком 32340: 10...
3 - ответьте на пару вопросов, ! 1. как террористы обосновывают себя, свои...
1 - 1)тепловой эффект реакции образования оксида железа(3) из железа и кислорода=1642,6...
2 - Напишитк предложения со словами сами tourist destination, transfer, transport,...
2 - Напишите сами на предложения со словами pyramid, ramp, ruler, slave, square,...
3 - Предложения со словами dirt, drawing, farewell, farmer, form, journey,...
3 - Оксид серы (4) взаимодействует с каждым из двух веществ: 1)h3po4,co 2)...
1 - 5процентов задуманного числа увеличели на 14,2,затем результат увеличили...
3 - Сообщение про одного художника их серебреннего века мхк...
2
в)
по частям:
г)
с неопределенных коэффициентов:
система:
получаем: