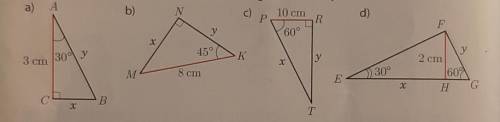
Найти неизвестные стороны (x, y) в данных прямоугольных треугольниках. Если есть решение хотя бы 1 треугольника, буду очень благодарна.
Другие вопросы по теме Математика
Популярные вопросы
- Умоляю мне , мне нужно ......
3 - Зробіть кр будьласкв алгебра 8 клас 1варіант...
1 - 7. Чому пані Бартолотті, Eroн і Кіті не захотіли повернути Конрада в«ідеальне...
2 - .Розрахуйте рівень безробіття:кількість трудових ресурсів області-400 тис.осіб,із...
1 - Захириддин Мухаммад Бабур – правитель, известный узбекский поэт, ценитель и...
2 - Какой объем углекислого газа (н.у.) получится при сжигании 8 г этана в 6,72...
1 - Твір усмішка написати меми ...
3 - Завтра переводной экзамен, а я забыла как решать......
2 - Як була ликвидована Запорижська сич?...
2 - ведро с песком весом 240Н поднимают с не подвижного блока на высоту 10м, действуя...
2
a) х = √3 см, у = 2√3 см, или CB = √3 см, AB = 2√3 см.
b) х = 4√2 см, у = 4√2 см, или NM = 4√2 см, NK = 4√2 см.
c) х = 20 см, у = 10√3 см, или PT = 20 см, RT = 10√3 см.
d) х = 2√3 см, у = 4√3/3 см, или EH = 2√3 см, FG = 4√3/3 см.
Пошаговое объяснение:
а) Катет равен другому катету, умноженному на тангенс угла, противолежащего данному катету:
х = 3 * tg 30° = 3 * (√3/3) = √3 см,
у = 2х = 2√3 см, т.к. катет, лежащий против угла 30°, равен половине гипотенузы.
ответ: х = √3 см, у = 2√3 см, или CB = √3 см, AB = 2√3 см.
b)
∠М = 180°-∠N-∠K =180°-90°-45° =45°,
т.к. ∠М = ∠K = 45°, то ΔMNK - равнобедренный и х = у.
Катет равен гипотенузе, умноженной на синус угла противолежащего этому катету:
х = 8*sin45° = 8 * (√2/2) = 4√2
ответ: х = 4√2 см, у = 4√2 см, или NM = 4√2 см, NK = 4√2 см
c)
∠Т = 180°-∠R-∠P = 180°-90°-60° =30°,
PR = 10 cм и лежит против угла в 30°, значит он равен 1/2 гипотенузы х, откуда х = 10* 2 = 20 см;
Катет равен гипотенузе, умноженной на синус угла противолежащего этому катету:
у = 20 * sin60° = 20 * (√3/2) = 10√3 см.
ответ: х = 20 см, у = 10√3 см, или PT = 20 см, RT = 10√3 см
d)
В прямоугольном ΔEFH катет FH лежит против угла 30°, следовательно, гипотенуза EF этого треугольника равна 2FH :
EF = 2* FH = 2* 2 = 4 см;
отсюда х = √(EF²- FH²) = √(4²- 2²) = √(16 -4) = √12 = 2√3.
В прямоугольном ΔFGH катет GH равен другому катету FH, умноженному на тангенс угла, противолежащего этому катету (а угол HFG = 30°):
GH = FH *tg 30° = 2 * (√3/3) = (2√3)/3 см;
отсюда
у = √(FH²+HG²) = √(2²+(2√3/3)²) = √(4 + 4*3/9) = √(36+12)/9= √48/9= √(16*3) /9= 4√3/3 см
ответ: х = 2√3 см, у = 4√3/3 см, или EH = 2√3 см, FG = 4√3/3 см