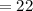Найти наименьшее значение функции y(x)=3-cos x-48/pi x+19 на отрезке (-2pi/3 ;0)
Другие вопросы по теме Математика
Популярные вопросы
- Как проявилось на карте мира государство Израиль...
1 - Известно, что элементы образуют базис линейного пространства. См. картинку...
3 - В соответствии с чем осуществляется разработка международного стандарта...
1 - Зменште число 68,7 на суму чисел 44,7 и0, 375...
1 - С графика функции y = + 4х + 3 установите ее свойств. .уИНТАОбласть определения...
1 - Знайти суму перших десяти членів арифметичної прогресії (аn): -3; 4; 11…...
1 - 1.«Орлеанской девой» прозвали девушку по имени 2. Основоположником абсолютной...
3 - дечку масу газу закрито при 320 К і тиску 10⁵ Па. Яким буде тиск газу, якщо...
1 - 108 км/год - ? м/с б) 360 дм/хв - ? м/св) 5400 см/хв. - ? м/сг) 30 м/с - ?...
1 - 1126. Обчисліть: 1)-5 - 15-(-28) – 14;5) -3-(-2,2) - (3)6) 10%-(-44)-37-(-5)2)...
2
Пошаговое объяснение:
нет корней, так как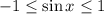 , а
, а 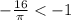
значит,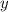 наим
наим