Найти наименьшее значение функции y=x^3/3-4x на отрезке [-6;3]
Другие вопросы по теме Математика
Популярные вопросы
- Твір на тему засудження комплексу меншовартості національного безпамятства...
2 - Почему рассказ называют малым прозаическим произведением? ...
1 - Черчение. Нужно сделать разрез 1\4 детали в аксонометрии (3д заранее благодарю!...
2 - Кластер на тему призвание...
2 - Replace what is given in bold type by infinitive phrases....
3 - На координатной плоскости постройте точки: А(-2; 4), B(-1; -3), C(-1; 5;...
3 - 2 complete the text with the words exercize 1...
2 - х/e4+sin2x х числитель e4 знаменатель...
3 - Українці розуміють росіян а чи росіяни розумцють українців...
3 - Почему лишняя хромосома в одной паре приводит к негативным последствиям,...
2
Пошаговое объяснение:
f'(x)=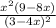
x²=0
x₁=0
9-8x=0
-8x= -9
x= -9:(-8)
x₂=1,125
3-4x≠0
-4x≠ -3
x≠0,75
y наимен.= -8