Найти наибольшее и наименьшее значение функции
на заданных отрезках.
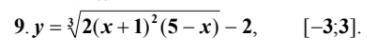
Другие вопросы по теме Математика
Популярные вопросы
- Написать сочинение рассуждение( развернуть ответ на вопрос) на вопрос:...
2 - 8класс вычислите массу и количество вещества гидроксид калия...
3 - Есепке комектесіп жібересіздер ма...
1 - Present континиус употребляется для описания действия которые происходят...
1 - Полезны ли магнитные бури ? ( дать желательно развернутый ответ)....
3 - Что общего между реакциями в органической и неорганической ?...
1 - Сходства и различия режимов муссолини и нацистского. кратко)...
1 - Водинаковых по массе ящиках 35кг яблок. сколько кг яблок в з таких...
1 - Группа студентов случайным образом делится на 2 части и отправляется...
3 - 7)что с точки зрения объединяет перечисленные в ряду элементы ?...
2
Найдем сначала наибольшее и наименьшее значения функции
y=(x+1)²(5-x). В силу того, что функция извлечения корня третьей степени монотонно возрастает, достаточно будет затем умножить найденные значения на 2, извлечь корень третьей степени из получившихся чисел, после чего вычесть из них 2.
Внутри интервала (-3;3) лежит один из нулей производной - это x=-1. Найдем значения функции в точках -3; 3 (концах отрезка) и в точке -1:
y(-3)=y(3)=32 - наибольшее значение; y(-1)=0 - наименьшее значение.
Осталось с получившимися числами проделать указанные операции - умножить на 2, извлечь корень третьей степени и вычесть 2:
ответ: наибольшее значение равно 2 и достигается на концах отрезка, наименьшее значение равно минус 2 и достигается в точке минус 1.
Достаточно найти точки х на которых
(х+1)^2*(5-x) принимает наибольшее и наименьшее значения .
Дифференцируем.
2(х+1)*(5-х)-(х+1)^2
Нули этой функции те же, что и у
2(х+1)*(5-х)-(х+1)^2=(х+1)*(10-2х-х-1)=-(х+1)(9-3х)
Производная равна 0 в точках х=-1 и х=3
Значит локальные экстремумы (или точки перегиба) находятся в этих точках.
В пределах отрезка два возможных экстремума в точке х=-1 и х=3.
Конечно, можно убедиться, что в этих точках производная меняет знак, поэтому это экстремумы.
Однако, достаточно посчитать значения функции в этих точках и на краях отрезка :
у(-3)=(2*4*8)^(1/3)-2=2
y(-1)=-2
y(3)=(2*16*2)^(1/3-2=2
Итак функция принимает два равных максимальных значения при х=3 и х=-3 и минимальное значение при х=-1.
Максимальные значения равны 2. Минимальное значение равно -2.
Здесь ^ -возведение в степень.