Найти линии уровня функции
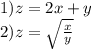
Другие вопросы по теме Математика
Популярные вопросы
- Софія має 52 однакові прямокутні рівнобедрені трикуктники вона хоче скласти...
3 - 6. Лодка плыла по течению 1,5 часов и 2,3против течения. Найдите весь путь...
2 - Розкажіть методи підстановки систему лінійних рівнянь ( х-зу=8 ( 2х-у=6Це...
2 - ОЧЕНЬ Напишите уравнение реакций катодного и анодного процессов, протекающих...
1 - Сколько запятых нужно поставить в предложении? Наспех павячэраўшы мы наслали...
2 - Pнайти критичні точки функції та найбільше і найменше значення на відрізку...
2 - У сегмент, дуга якого дорівнює 120° і має довжину a, вписано коло найбільшого...
1 - 09.07.2016г. Синицын Р.В. заключил трудовой договор с ООО «Лесные согласно...
3 - Чи вистачить 20 л водню (н. у.) для відновлення 8 г купруму (||) оксиду...
2 - Определи значение переменной k, при котором разность дробей 1/(k−8) и 5/(k+8)...
1
Найти область определения функции: z(x,y)=√{ln (x2+2y-1)}. ... Рис. 2. Линии одинакового уровня функции z(x,y)={x2}/{4}-{y2}/{9} ... +{1}/{2!}(fx2”(x0,y0)Δ x2+ 2fxy”(x0,y0)Δ x Δ y+ fyy”(x0,y0)Δ y2 )+ ... z}{\partial y}dy\;\text{или}\;dz=d_xz+d_yz , $$ где $d_xz=\dfrac{\partial z}{\partial x}dx,\;d_yz=\dfrac{\partial z}{\partial y}dy$ ...