Найти кратчайшее расстояние от точки A(6,-8) к окружности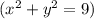
Другие вопросы по теме Математика
Популярные вопросы
- С каким из этих двух определений вы согласны? Политический режим –...
2 - Согласны ли вы с мнением русского историка Н. М. Карамзина: «Демократическое...
2 - Какую роль играли авторитарные режимы в развитии общества, можно ли...
3 - В мире насчитывается около 200 государств и до 5 тысяч этносов, из...
1 - В истории античного мира прочтите о ранней греческой тирании. В чем...
2 - Что такое гражданское общество? Почему его надо понимать в двух значениях?...
1 - Подумайте, какие особенности российской политической системы и традиций...
2 - Подробно опишите республиканский тип правления государства. Какую функцию...
1 - Почему в мировой истории вокруг проблемы гражданства происходили не...
1 - Приведите примеры диктатуры и дайте ее характеристику....
3
7
Пошаговое объяснение:
Задание.
Найти кратчайшее расстояние от точки A(6,-8) к окружности (х²+y²= 9).
Решение.
1) Уравнение х²+y²= 9 описывает окружность радиуса R = √9 = 3, с центром в точке О (0;0), т.к. а = 0 и b = 0.
2) Соответственно кратчайшим расстоянием между точкой А (6; -8) и радиусом данной окружности будет разность между длиной отрезка ОА и радиусом данной окружности, равным 3.
3) Находим длину отрезка ОА:
ОА = √(6²+(-8)²=√(36+64)=√100 = 10.
4) Кратчайшее расстояние от точки A(6,-8) к окружности (х²+y²= 9) равно: 10 - 3 = 7.
ответ: 7.