1. Математика
  2. Найти корни уравнения:

Найти корни уравнения: \dfrac{3}{(x+3)(x-1)} -\dfrac{4}{(x+4)(x-2)} =-\dfrac{1}{2}

Удача575 Удача575    2   24.05.2019 17:18    0

Ответы
viktordro95 viktordro95  20.06.2020 16:40

x_{1} = -1+\sqrt{14}; x_{2} = -1-\sqrt{14}; x_{3}=0; x_{4} =-2

Пошаговое объяснение:

1) Перенесем -1/2 в левую часть и приведем выражение к общему знаменателю:

\frac{3*2(x+4)(x-2) - 4*2(x+3)(x-1) + (x+3)(x-1)(x+4)(x-2)}{2(x+3)(x-1)(x+4)(x-2)}=0

2) Найдем ОДЗ:

2(x+3)(x-1)(x+4)(x-2)\neq 0\\ x\neq -3; x\neq 1; x\neq -4; x\neq 2

3) Упростим выражение:

3*2(x+4)(x-2) - 4*2(x+3)(x-1) + (x+3)(x-1)(x+4)(x-2) = 6(x^{2}+4x-2x-8) - 8(x^{2}+3x-x-3) + (x^{2}+3x-x-3)(x^{2}+4x-2x-8) = 6(x^{2}+2x-8) - 8(x^{2}+2x-3) + (x^{2}+2x-3)(x^{2}+2x-8)

4) Пусть (x^{2}+2x) = t, тогда:

6(x^{2}+2x-8) - 8(x^{2}+2x-3) + (x^{2}+2x-3)(x^{2}+2x-8) = 6(t-8) - 8(t-3) + (t-3)(t-8) = 0\\ 6t-48-8t+24+(t^{2}-3t-8t+24)=0\\ -2t-24+t^{2}-11t+24=0\\ t^{2}-13t=0\\ t(t-13)=0\\ t=0;t=13

5) Подставим полученные значения в замену и найдем х:

а)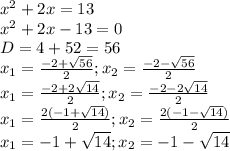 x^{2}+2x=13\\ x^{2}+2x-13=0\\ D=4+52 = 56\\ x_{1} = \frac{-2+\sqrt{56} }{2}; x_{2} = \frac{-2-\sqrt{56} }{2}\\ x_{1} = \frac{-2+2\sqrt{14} }{2}; x_{2} = \frac{-2-2\sqrt{14} }{2}\\ x_{1} = \frac{2(-1+\sqrt{14}) }{2}; x_{2} = \frac{2(-1-\sqrt{14}) }{2}\\ x_{1} = -1+\sqrt{14}; x_{2} = -1-\sqrt{14}

б) x^{2}+2x = 0\\ x(x+2)=0\\ x_{3}=0; x_{4} =-2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
lilik03 lilik03  18.11.2020 07:07
Одписки Выполни задание1 Выясни с чертёжного угольника, какой из отрезков МР, МТ, МО, изображённына рисунке, является перпендикуляром, проведённым из точки М к прямой АС.2 Проведи...
Papyas3 Papyas3  18.11.2020 07:07
При какой значении х верно равенство...
olgakoryakina olgakoryakina  18.11.2020 07:06
Пропорцияның белгісіз мүшесін тап: 6–6–55АртқаТексеру​...
машуля5552 машуля5552  18.11.2020 07:06
Если 8530000умножить на 4,4 число будетзаписыватся под цифрой ?...
anna7251 anna7251  18.11.2020 07:06
Функция задана формулой у=2x-1.какое значение у соответствует х, равному -4, 5? ​...
levusvaleria levusvaleria  18.11.2020 07:06
5/26 және 6/25 сандар аралығына тиісті бөлшекті тап ​...
LisenokLove2003 LisenokLove2003  18.11.2020 07:06
Известно, что m b c u. Сравни дроби: ответ: Назад Проверить...
Camall Camall  18.11.2020 07:06
(5 5/17+х)*(5 1/9-2 5/18)=0...
KattyDark010203 KattyDark010203  18.11.2020 07:06
С вершины угла KLO перпендикулярно к биссектрисе LP этого угла прове-ден луч LA. Найдите углы между лучом LA и сторонами данного угла KLO, если KLO = 42⁰?...
IVANICH31 IVANICH31  18.11.2020 07:06
X = -0,2 болса, f(x) = 12 + 5x мәнін тап.​...

Популярные вопросы