Найти коэффицент при 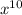
в разложении
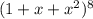
Другие вопросы по теме Математика
Популярные вопросы
- Какие цветки называются двуполыми, а какие однополыми?...
2 - Спробуйте у вигляді схеми показати Житомирщину у складі більших...
1 - У двох довгих паралельних дротах, відстань між якими d = 8см,...
1 - Вычислить значение y=4x при 10 значении x. Шаг параметра цикла...
1 - 5 примеров вычислительных экспериментов...
1 - 5. а) Соедините линиями и покажите логические цепочки: «материал...
1 - Испанский или португалиский завоеватель на американском континенте...
2 - Почему ускорение свободного падения не совпало с ранним? причины?...
3 - Порівняння природи та занять Дворіччя, Єгипету, Фінікійців,...
3 - Раскрой скобки: (x−8)⋅(x−7)....
1
784
Пошаговое объяснение:
Согласно полиномиальной формуле,
Тогда коэффициент при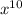 равен
равен 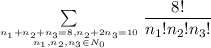
При этом, очевидно,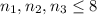
А тогда