1. Математика
  2. Найти х при которых если

Найти х при которых если не сложно) ​

Maowsk Maowsk    3   17.04.2020 01:13    0

Ответы
кпеп кпеп  13.10.2020 09:55

x \in [0;+\infty)

Пошаговое объяснение:

f(x)=(x+2)^2\cdot \sqrt{x}\\f'(x)=2(x+2)\cdot \sqrt{x}+\frac{1}{2\sqrt{x}}\cdot(x+2)^2=\frac{4x(x+2)+(x+2)^2}{2\sqrt{x}}

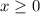
ОДЗ: x \geq0

4x(x+2)+(x+2)^2=(x+2)(4x+x+2)=(x+2)(5x+2) 0

Видно, что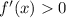 f'(x)0 для любого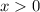 x0

Другой

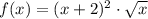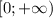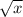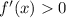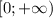Функция f(x)=(x+2)^2\cdot \sqrt{x} является произведением двух возрастающих функций на промежутке [0;+\infty) (промежуток появляется из-за ОДЗ на функцию \sqrt{x}). Отсюда следует, что и сама функция является возрастающей, т.е. f'(x)0 на промежутке [0;+\infty) .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kiryazhigulski kiryazhigulski  20.03.2019 15:20
Расстояние 966м мирас преодолевает за 10мин, а дархан-за 12мин. с какой скоростью они будут сближаться, если будут идти навстречу друг другу?...
Гоша2285 Гоша2285  20.03.2019 15:20
Вырази в квадратных метрах: 17000см в квадрате+18000см в квадрате - 50 дм в квадрате=? в литрах: (1300дм в кубе -400дм в кубе): 10+5метров в кубе 1-4 класс !...
викусик152 викусик152  20.03.2019 15:20
Обьясните как решать эти 2 ! 1)масса бочки с водой 94,5 кг.какова масса бочки,если она в 6,5 раза меньше массы налитой в ней воды? 2)один из штабелей лесного сада состоит...
Sa4eR Sa4eR  20.03.2019 15:20
Сфинксы на египетском мосту ! какой греческий образ?...
Соска997 Соска997  20.03.2019 15:20
Знайти значення виразу а: 9,якщо а=18,а=45...
amir3009 amir3009  20.03.2019 15:20
Мария сплела браслет и бусы.для бус ей понадобилось бусинок в 7 раз больше,чем для браслета.после окончания работы осталось 127 бусинок.сколько бусинок пошло для браслета...
BrainS711 BrainS711  20.03.2019 15:20
Решите . мы проходим тему степень числа.квадрат и куб числа.найдите значение выражений: е)(17-16)на верху маленькая 8 +2 на верху 5 ж)10 на верху 6 -20 на верху 4 з)3 на...
Тима77711 Тима77711  20.03.2019 15:10
Урожайность-это масса урожая растений,собранного с единицы площади.обозначив урожайность буквой m, площадь s, запишите формулу для нахождения массы м урожая.определите по...
raxievali raxievali  20.03.2019 15:10
Выпишите сначало точные числа, а затем приближенные: в коробке 9 карандашей; во дворе посадили 17 деревьев; глубина реки 31 метр; высота горы 279 метров; в кватрире живет...
F1kser F1kser  20.03.2019 15:10
Во всех цехах кондитерской фабрики работает 312 человек.ы3-х цехах работает по 24 человека,а в остальных по 30 человекюсколько всего цехов на кондитерской фабрике?...

Популярные вопросы