Найти границу, используя правило Лопиталя 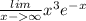
Безумно буду благодарен

Другие вопросы по теме Математика
Популярные вопросы
- Написать сочинение о необычном празднике....
2 - Решите уровнение х*5000/5=2000 другое если что это диление /...
3 - 13 как произнести это предложение : to look after smb / smth...
1 - 2. в содержится газ при температуре 17 градусов и давление 1мпа....
2 - Пусть a-1/a=2/3 найдите (a^12+1)/a^6...
3 - Решить 4 класс стр44 №5 учебник за 4 класс алматы атамура 2015...
2 - Спиши .подчеркни твердые согласные синим карандашом, мягкие...
2 - Найдите сумму первых 20 членов арифметической .прогрессии.:...
1 - Начертить четырехугольник у которого три угла прямые,является...
2 - Написать биографию про мирский замок по...
1
0
Пошаговое объяснение:
Т.к. неопределенность, то пользуемся правилом Лопиталя: