1. Математика
  2. Найти градиент скалярного поля

Найти градиент скалярного поля u(x, y, z) в точке м0(2,1,1).вычислить производную этого поля в точке м0 по направлению вектора i=-2i+j-k

кекай кекай    2   26.09.2019 23:50    0

Ответы
ivanovgeorg123георг ivanovgeorg123георг  08.10.2020 21:34

1) grad\ u=\frac{\partial u}{\partial x} \vec{i} +\frac{\partial u}{\partial y} \vec{j} +\frac{\partial u}{\partial z} \vec{k}

u=x+\ln(y^2+z^2)\\ \frac{\partial u}{\partial x} =1;\ \frac{\partial u}{\partial y} =\frac{2y}{y^2+z^2} ;\ \frac{\partial u}{\partial z} =\frac{2z}{y^2+z^2} \\ M_o(2;1;1) \Rightarrow x=2;\ y=1;\ z=1 \\ \frac{\partial u}{\partial x} (M_o) =1;\ \frac{\partial u}{\partial y} (M_o) =\frac{2*1}{1^2+1^2}=1;\ \frac{\partial u}{\partial z} (M_o) =\frac{2*1}{1^2+1^2}=1;

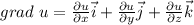
Градиент u в точке (2;1;1):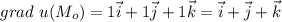 grad\ u (M_o)= 1 \vec{i} + 1 \vec{j} + 1 \vec{k} = \vec{i} + \vec{j} + \vec{k}

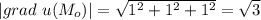
2) |grad\ u(M_o)| = \sqrt{1^2+1^2+1^2} =\sqrt{3}

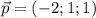
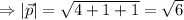
Для вектора \vec{p}=(-2;1;1) \Rightarrow |\vec{p}|=\sqrt{4+1+1} =\sqrt{6}

Направляющие углы:

\cos \alpha =\frac{-2}{\sqrt{6}} ;\ \cos \beta =\frac{1}{\sqrt{6}} ;\ \cos \gamma =\frac{-1}{\sqrt{6}}

Производная поля в точке (2;1;1) по направлению вектора р:

\frac{\partial u}{\partial p} =\frac{\partial u}{\partial x}(M_o) \cos \alpha +\frac{\partial u}{\partial y}(M_o) \cos \beta +\frac{\partial u}{\partial z}(M_o) \cos \gamma =\\ = 1 \cdot (-\frac{2}{\sqrt{6}} )+1 \cdot \frac{1}{\sqrt{6}} +1 \cdot (-\frac{1}{\sqrt{6}} )=-\frac{2}{\sqrt{6}} =-\frac{\sqrt{6}}{3}


Найти градиент скалярного поля u(x, y, z) в точке м0(2,1,1).вычислить производную этого поля в точке
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Sonta0004 Sonta0004  26.06.2019 10:20
Вмоскве живёт около 100 000 ивановых,а смирновых на 20 000 меньше.сколько ивановых и смирновых живёт в москве?...
alisabugor alisabugor  26.06.2019 10:20
Одна бригада может собрать весь урожай ягод с участка площадью 48 соток за 6 дней, а другая-за 3 дня. за сколько дней собрали бы весь урожай с этого участка обе бригады при вместимость...
crasheftf crasheftf  26.06.2019 10:20
Для вышивания приобрели мулене двух видов: по цене 5р. и 11 р. 40к. за моток,всего 32 мотка.сколько мотков того и другово вида было приобретено,если один мотокстоил 9р.?...
StrawberryCake StrawberryCake  26.06.2019 10:20
Даны числа 709; -21; 0; 3,7; -0,98; 1 2/5 установить, какие их них принадлежат множеству: 1) натуральных чисел, 2) целых чисел, 3) рациональных чисел, 4) действительных чисел...
GolduckChannel GolduckChannel  26.06.2019 10:20
Сколько процентов составляет одна восьмая дробь?...
Craftrik Craftrik  26.06.2019 10:20
Выделить у дроби целую час: 45/7, 28/5, 91/15, 56/11....
Діана25123456789000 Діана25123456789000  26.06.2019 10:20
Некто израсходовал половину своих денег и 1/3 остатка . после этого у него осталось 6 рублей. сколько денег было у него первоначально. с объяснением....
aza54 aza54  26.06.2019 10:20
Проверьте,является ли пропорцией данное равенство: а)0,5: 1,7=17: 5 б)0,3/2,7=0,1/0,9...
Kachmaresghg Kachmaresghg  26.06.2019 10:20
Сколько будет в 50-60+99•103 учебник 7 класса с. 49 n 4 „б”...
Мозговина12 Мозговина12  26.06.2019 10:20
2брата нашли по 5 грибов.сколько всего грибов нашли братье? 2 .в 6 клетках по 2 обезьяны.сколько всего обезьян в этих клетках?...

Популярные вопросы