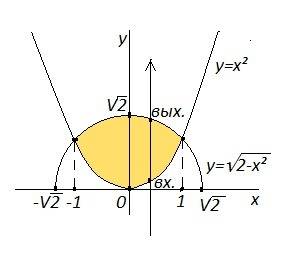
Найти двойной интеграл по облости d f(x,y)dxdy d: y=√2-x², y=x²
Ответы
Точки пересечения полуокружности у=√2-х² и параболы у=х² :
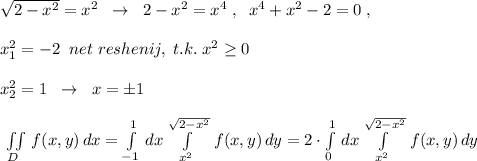
ПОКАЗАТЬ ОТВЕТЫ
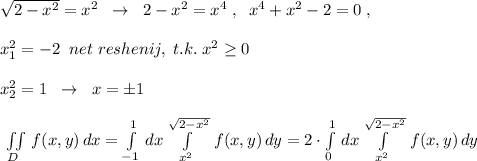

Другие вопросы по теме Математика
Популярные вопросы
- Разобрать слова по составу передвегаются...
3 - Переведите ! без переводчика in deutschland sind 10 schuljahre pflicht. danach...
1 - 1. реши . от огорода до посёлка автобус ехал 2 часа мо скоростью 75 км/ч. сколько...
3 - Примеры слов с беглыми гласными(е) не менее 10 слов...
3 - +10005000 . найдите закономерность 234 (111) 567 422 947...
1 - Акак понять безошибочно списать текст, его просто списать, слова не надо переделывать...
1 - Списать предложения, 1-2 предложения подчеркните мягкие согласные. 3-4 предложении...
2 - Точки м и n являются серединами сторон ав и вс треугольника авс, сторона ас...
1 - Объясните словосочетание чтение роскошь...
3 - Сиз танертенгилик жаттыгумен шугылданасыз ба? сиз спортпен айналасыз ба? алматыдагы...
2