Найти длину окружности около которой описана равнобедренная трапеция с основаниями 2 и 8 см

ответ:    12.56 см.

Пошаговое объяснение:

В трапецию можно вписать окружность, если сумма оснований равна сумме ее боковых сторон.

ABCD - трапеция. ВС+AD=AB+CD=2+8=10 см.

Боковые стороны АВ=CD=10/2=5 см .  

Высота трапеции равна диаметру вписанной окружности находим по т. Пифагора  AH=(AD-BC)/2=(8-2)/2=6/2=3 см.

D= ВН=√(АВ²-АН²)=√(5²-3²)=√(25-9)=√16=4 см.

Длина окружности С=πD=3.14*4= 12.56 см.

Если равнобедренная трапеция описана около окружности, значит, сумма её оснований равна сумме боковых сторон. Трапеция равнобедренная, значит, боковые стороны равны. Отсюда:

1) - длина боковой стороны трапеции.

Далее проведём высоты трапеции, исходящие из вершин верхнего основания. Получаем, что нижнее основание трапеции делится на три отрезка, равные 3, 2 и 3 см соответственно. Имеем прямоугольный треугольник, где боковая сторона трапеции = 5 - гипотенуза, а один из катетов = 3 - часть нижнего основания трапеции, отделённая высотой.

Тогда из прямоугольного треугольника по теореме Пифагора имеем:

2) , где x^2 - высота трапеции, что равна диаметру окружности.

4 см - длина высоты, равной диаметру. Диаметр вдвое больше радиуса, тогда:

3)

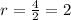
Найдём длину окружности:

4)

pi ≈ 3,14

C ≈ 4*3,14 ≈ 12,56 см

12,56 см.