Найти длину дуги кривой φ=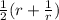 от r=1 до r=3 С РЕШЕНИЕМ (В полярных координатах, r-полярный радиус, φ - полярный угол) ( задача 1684 из Демидовича для втузов(4 издание) )
от r=1 до r=3 С РЕШЕНИЕМ (В полярных координатах, r-полярный радиус, φ - полярный угол) ( задача 1684 из Демидовича для втузов(4 издание) )
Другие вопросы по теме Математика
Популярные вопросы
- Составить предложение на тему добрые дела красят человека, и розобрать его по...
1 - Умиши 45 рублей . девятую часть этих денег он потратил на покупку ластика , а...
3 - Запишите в виде степени с основанием а: (а в n-ой степени)в 3-ей степени...
1 - Решение неравенство: 1)5x+10 3x+2 2)4(y-2)больше равно 5(y-3) 3)2(x+8)-5x 4-3x...
1 - А) запиши двухзначные числа,которые меньше 18....
1 - Укандрата куртка коротковата. какие звуки повторяются...
1 - Лисиця наловила окунів та розклала їх на 5 купок,таким чином,що у всіх купках...
1 - Масса 1 л воды равна 1 кг , а 1 л бензина - на 270 г меньше .найдите массу 1...
1 - Какое из чисел 516и 615 расположено на координатном луче левее...
1 - Почему любовь мизгиря и снегурочки была обречена...
1
α=(1/2)*(r+1/r)
Используем формулу длины дуги кривой (1),
/не нашел фи, вместо нее в формулу поставил альфа/, получим
α'=(1/2)*(1-(1/r²))=1/2-(1/(2r²)
α'²=(1/4+(1/(4r⁴))-1/(2r²))
r²α'²+1=(r²/4)+(1/(4r²))-(1/(2)+1=(r²/4)+(1/(4r²))+(1/(2)=((r/2)+(1/(2r)))²
√((r/2)+(1/(2r)))²=(r/2)+(1/(2r)
Подставим пределы интегрирования. получим 3²/4+(ln3)/2-(1/4-ln1)=
8/4-(ln3)/2=2-(ln3)/2