Найти диагонали прямоугольника abcd,если < cad=30 градусам ,cd=15 см.
Другие вопросы по теме Математика
Популярные вопросы
- А)1/3 |x| +3/7 |x|- 8,5=7,5б) (3,4x -2) + 8 = 4...
1 - На рисунках представлены различные организмы. Определите, по какому признаку...
3 - 125М⁴Р⁶÷(-0,5М⁴Р³)÷ 125МР²...
2 - 3. Составь простой план текста. ( ) Опираясь на план, кратко изложи его...
2 - Вот на фото тут все видно можно побыстрее ответы...
1 - Please help me with essay...
1 - Правильно составить предложения...
1 - Fill in the blanks below to complete the sentences. Study the boxes above....
1 - Какие постройки сооружали жители разных частей света в эпоху древнего мир...
3 - Упражнение 1. Распределите глаголы на правильные и неправильные. Watched,...
2
Дано: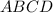 — прямоугольник ⇒
— прямоугольник ⇒ 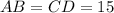 см,
см, 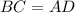 ;
; 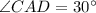 .
.
Найти: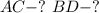
Решение. По свойству прямоугольника его диагонали равны: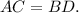 Одна его диагональ делит прямоугольник на два равных прямоугольных треугольника.
Одна его диагональ делит прямоугольник на два равных прямоугольных треугольника.
Рассмотрим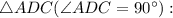
ответ: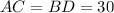 см.
см.