Найти целые значения параметра m, при которых уравнение имеет ровно два решения. Если таких значений несколько, запишите в ответ их сумму.

Найти целые значения параметра m, при которых уравнение имеет ровно два решения. Если таких значений

Ответы

perizatttt 18.08.2021 14:07

-8

Пошаговое объяснение:

ОДЗ: $\begin{equation*}\begin{cases}2x-30,\\2x-3\neq 1,\\x^2+mx+110\end{cases}\end{equation*}$ $\begin{equation*}\begin{cases}x1{,}5,\\x\neq 2,\\x^2+mx+110\end{cases}\end{equation*}$

Тогда уравнение равносильно следующему:

$(2x-3)^{\log_{2x-3}{(x^2+mx+11)}}=(2x-3)^0\\x^2+mx+11=1$

Так как мы ищем x, удовлетворяющие такому равенству, условие x^2+mx+110 выполняются автоматически.

$x^2+mx+10=0\\D=m^2-400\Leftrightarrow m\in(-\infty;-2\sqrt{10})\cup(2\sqrt{10};+\infty)$

Учтём ограничения. Если x ≠ 2, то равенство $2^2+2m+10=0\Leftrightarrow m=-7$ не выполняется, значит, m ≠ -7.

Для учёта первого ограничения найдём корни уравнения:

$x_1=\dfrac{-m-\sqrt{m^2-40}}{2},x_2=\dfrac{-m+\sqrt{m^2-40}}{2}\\x_1$

Если x₁ > 1,5, то x₂ также будет больше 1,5.

$\dfrac{-m-\sqrt{m^2-40}}{2}\dfrac{3}{2}\\m+\sqrt{m^2-40}$

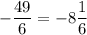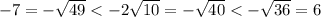Учитывая ограничения дискриминанта, -2√10 < -3, а также m ≠ -7 (находится между $-\dfrac{49}{6}=-8\dfrac{1}{6}$ и $-7=-\sqrt{49}$ ), получаем $m\in\left(-\dfrac{49}{6};-7\right)\cup\left(-7; -2\sqrt{10}\right)$ . Целые значения параметра m: -8.