Найти алгебраическую и тригонометрическую формы числа z = z1+z2. Изобразить числа z1, z2, z на комплексной плоскости. Вычислить z12 по формуле Муавра.
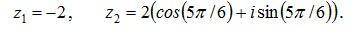
Другие вопросы по теме Математика
Популярные вопросы
- Сколько раз в жизни плодоносит малина...
2 - Монолог по языку как поступать в экстренных ситуациях...
1 - Розкласти на множники квадратний тричлен xквадрат-x-42...
2 - Составить план к рассказу русалочка из 20 пунктов...
2 - Записать в системе «си» : 3,6 км/час = 5,7 кдж = )...
3 - Какая сама результативная колония британской империи в 19 веке?...
2 - То он блин, то он клин, ночью на небе один. скажите....
1 - Все решили во что бы то ни стало собрать коллекцию цветов для гербария.боялись...
3 - 1год-24хв= 4м-39см= 5м÷2= 3дм-26см= 2м÷5= 2м-8см=...
1 - Два данных угла так относятся как 1: 3,а смежные с ними-как 4: 3. найдите данные...
3
Для начала, давайте найдем алгебраическую форму числа z1 и z2. На комплексной плоскости, число z1 представляет собой вектор, который можно записать в виде a1 + b1i, где a1 - это действительная часть числа, а b1 - мнимая часть. Аналогично, число z2 можно записать в виде a2 + b2i.
Из заданной схемы видно, что a1 = 1, b1 = 2, a2 = -3, b2 = 4.
Теперь найдем алгебраическую форму числа z. Для этого нужно просто сложить соответствующие части чисел z1 и z2:
z = z1 + z2 = (a1 + a2) + (b1 + b2)i = (1 - 3) + (2 + 4)i = -2 + 6i
Таким образом, алгебраическая форма числа z - это -2 + 6i.
Теперь найдем тригонометрическую форму числа z. Для этого нужно найти модуль числа z и его аргумент. Модуль числа z можно найти по формуле |z| = sqrt(a^2 + b^2), где a и b - действительная и мнимая части числа соответственно. В нашем случае, a = -2 и b = 6, поэтому модуль числа z равен:
|z| = sqrt((-2)^2 + 6^2) = sqrt(4 + 36) = sqrt(40) = 2*sqrt(10)
Чтобы найти аргумент числа z, нужно воспользоваться формулой atan(b/a), где a и b - действительная и мнимая части числа соответственно. В нашем случае, a = -2 и b = 6, поэтому аргумент числа z равен:
arg(z) = atan(6/(-2)) = atan(-3) = -1.2490458...
Таким образом, тригонометрическая форма числа z - это 2*sqrt(10)(cos(-1.2490458...) + i*sin(-1.2490458...)).
Теперь давайте изобразим числа z1, z2 и z на комплексной плоскости. Для этого нужно найти их координаты в декартовой системе координат.
Для числа z1, координаты равны (1, 2).
Для числа z2, координаты равны (-3, 4).
Для числа z, координаты равны (-2, 6).
Постройте на плоскости систему координат и отметьте точки с указанными координатами.
Наконец, давайте вычислим z12 по формуле Муавра. Формула Муавра гласит, что (r1 * (cosθ1 + i*sinθ1)) ^ n = r1^n * (cos(nθ1) + i*sin(nθ1)), где r1 - модуль числа, θ1 - аргумент числа, а n - степень возведения.
В нашем случае, z1 имеет модуль 2*sqrt(10) и аргумент -1.2490458...
z12 = z1^2 = (2*sqrt(10))^2 * (cos(2*(-1.2490458...)) + i*sin(2*(-1.2490458...)))
z12 = 40 * (cos(-2.4980917...) + i*sin(-2.4980917...))
Таким образом, z12 имеет модуль 40 и аргумент -2.4980917...
Надеюсь, это подробное объяснение поможет вам понять, как найти алгебраическую и тригонометрическую формы числа z = z1 + z2, изобразить числа на комплексной плоскости и вычислить z12 по формуле Муавра. Если у вас все еще остались вопросы, не стесняйтесь задавать.