Найдите значение выражения: 5 + ctg82°30'
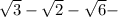
Другие вопросы по теме Математика
Популярные вопросы
- Цитатный план к сказке царевна лягушка...
3 - Напишите рассказ на школьную тему, озаглавив его одной из пословиц...
1 - Сколько героев в сказке легушка путешествиница...
2 - Скакой скоростью двигался поезд до начала торможения, если он тормозной...
2 - Сочинение на тему: по дороге в техникум...
2 - Объясните значение термина «прототип». кто стал прототипом учителя...
1 - Смартфон стоил 7.500 руб. сначала его цену снизили на 20 %, а затем...
3 - Найдите область определения функции f(x) = буду признательна: 3...
1 - Як побудувати графік функції y=x²+5|x|+6...
1 - Хотя бы один решите 1) |3-1,5x|=2,5 2) |1+3x|=2 3) |x^2-2|-2/2x+x^2...
2
-7
Пошаговое объяснение:
Довольно интересное задание, которое заставило меня подумать)
Для начала разберемся с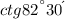 .
.
Известно, что в градусе, как и в часе 60 минут, поэтому это будет котангенс 82 градусов 30 минут, или котангенс 82,5 градусов: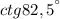
Данный котангенс можно представить в виде тангенса:
Далее, мы помним формулу: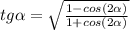
Преобразуем наш тангенс:
В свою очередь, косинус 15 градусов можно представить в виде:
А затем по формуле:
А эти косинусы можно найти в таблице:
Подставляем значения, получаем:
Затем, подставляя это значение в формулу (1) получим после некоторых преобразований:
Нам необходимо избавиться от корня. Домножим числитель и знаменатель на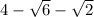
И запишем как: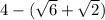 , что тоже самое, но в дальнейшем упростить.
, что тоже самое, но в дальнейшем упростить.
В итоге это будет выглядеть так:
Числитель можно представить в виде:
Вспоминая формулу квадрата разности: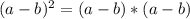 , имеем право числитель свернуть в квадрат разности.
, имеем право числитель свернуть в квадрат разности.
Знаменатель имеет вид:
Это ничто иное как разность квадратов:
Значит:
Теперь преобразуем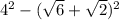 :
:
Вернемся к выражению под корнем:
Теперь домножим числитель и знаменатель на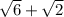 , числитель будет иметь вид:
, числитель будет иметь вид:
А знаменатель:
Возвращаемся к формуле (2):
Подставляем это значение в исходное выражение:
Это и будет итоговый ответ.