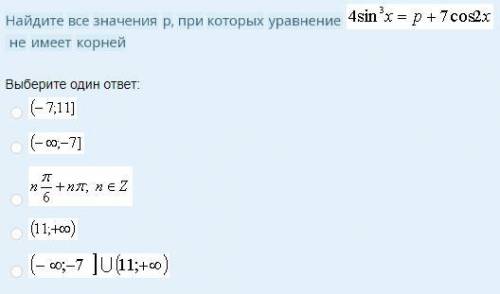
Найдите все значения р, при которых уравнение не имеет корней

Исследуем функцию f(u) =4u^3 + 14u^2 на отрезке от [-1;1]

Зануляется производная в точке u=0, второй нуль производной не принадлежит отрезку [-1;1]. Вторая производная в этой точке равна 28, значит это точка минимума.

В этой точке функция равна 0

На краях отрезка функция принимает значения 14-4 = 10 и 14+4 = 18. Максимальное значение 18

Значит если p+7>18 или p+7<0, корней нет

p>11 или p<-7

Это последний ответ. (ну только там опечатка наверное, -7 должна быть с круглой скобкой тоже)