Найдите все значения a, при которых уравнение 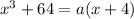имеет ровно два различных решения.

12; 48

Пошаговое объяснение:

Уравнение обязательно имеет одно решение: x = -4. Квадратное уравнение во второй скобке может иметь 0, 1 или 2 решения. Очевидно, нужно рассматривать последние два случая.

1. Если квадратное уравнение имеет одно решение, то оно должно отличаться от x = -4, так как требуется найти два различных решения.

2. Если квадратное уравнение имеет два решения, то одно из них должно равняться x = -4.

Случай 1:   — 1 решение.

При a = 12 — подходит.

Случай 2: — 2 решения, одно из них x = -4.

При a = 48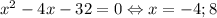 — подходит.