Найдите все натуральные числа, являющиеся решениями системы неравенств. 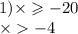
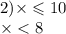
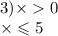
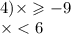
Другие вопросы по теме Математика
Популярные вопросы
- Одного человека спросили,сколько у него детей.ответ был такой:...
1 - Тани 12 лет саша 4 года во сколько раз таня старше саши 2) тани...
2 - Что нарисовать на тему добро и зло?...
1 - Диалог из 8 предложений на тему экскурсия в зоопарк...
1 - Где свободно мяч будет иметь большее ускорение: на первом этаже...
2 - Пришли второклассники в кафе 12мальчиков и 16девочек все сели...
3 - Сравнительная храктеристика царицы и царевны. царица и царевна....
3 - Из каких книг состоит библия и какие 10 заповедей христианства...
3 - Составное именное сказуемое грамматическое значение, значение...
3 - Стрех полей вывезли 4т капусты . с первого поля вывезли 1800кг...
3
Пошаговое объяснение: Натуральные числа- это целые и положительные числа, наименьшее натуральное число 1.
1)
х∈( -4 ;+∞)
ответ: х∈(1+∞)
2)
х∈(-∞;8).
ответ:х∈(1 ; 8)
3)
х∈(0 ;5]
ответ: х∈(1;5]
4)
х∈[-9;6)
х∈(1; 6).
В решении.
Пошаговое объяснение:
Найдите все натуральные числа, являющиеся решениями системы неравенств.
Натуральные числа - это те, с которых выражают целое количество предметов - два яблока, три апельсина. То есть натуральные числа это умное название для привычных всем чисел 1, 2, 3, 4 и так далее.
1) х >= -20
x > -4
Решение первого неравенства: х∈[-20; +∞);
Решение второго неравенства: х∈(-4; +∞).
Решение системы неравенств: х∈ (-4; +∞), пересечение.
Натуральные числа: 1,2,3,4,5,6, и т.д. до + бесконечности.
2) х <=10
x < 8
Решение первого неравенства: х∈(-∞; 10];
Решение второго неравенства: х∈(-∞; 8).
Решение системы неравенств: х∈ (-∞; 8), пересечение.
Натуральные числа: 1,2,3,4,5,6,7. (8 не входит в решения неравенства и системы, неравенство строгое).
3) x > 0
x <= 5
Решение первого неравенства: х∈(0; +∞);
Решение второго неравенства: х∈(-∞; 5].
Решение системы неравенств: х∈ (0; 5], пересечение.
Натуральные числа: 1,2,3,4,5. (5 входит в решения неравенства и системы, неравенство нестрогое).
4) x >= -9
x < 6
Решение первого неравенства: х∈[-9; +∞);
Решение второго неравенства: х∈(-∞; 6).
Решение системы неравенств: х∈ [-9; 6), пересечение.
Натуральные числа: 1,2,3,4,5. (6 не входит в решения неравенства и системы, неравенство строгое).