Найдите восьмой член геометрической прогрессии (bn), если b1=-2/27 и q=3.
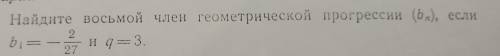
Другие вопросы по теме Математика
Популярные вопросы
- Логарифм 1/15 по основанию 5+ логарифм 1 по основанию 1/7...
1 - 3.луч nb делит прямой угол mnk на два угла так, что угол knb составляет 0,6 угла...
3 - Написать те глаголы которые часто призносят неправильно...
2 - Решите по действиям: 260*403-(568*5-1840) 671*223+(6000-87*40)...
1 - Схема государственное устройство сша по конституции 1787г напишите !...
3 - Выпишите те слова в которых выделенная гласная буква обозначает целый слог апельсин...
3 - Вычислите : (корень из 5-3)*корень из 14+6корень из 5 !...
2 - А1. укажи слова котором все согласные буквы обозначают мягкий звук 1) желе 2) пища...
1 - Расположите глаголы по степени усиления действия: пылать,гореть,пламенеть....
2 - Почему гекель финн лучший друг тома...
1
В данной задаче даны первый член b1 и знаменатель прогрессии q. Первый член равен -2/27, а знаменатель прогрессии равен 3.
Формула для нахождения n-го члена геометрической прогрессии: bn = b1 * q^(n-1)
Здесь bn - n-й член геометрической прогрессии, b1 - первый член геометрической прогрессии, q - знаменатель прогрессии, n - номер члена прогрессии, который мы хотим найти.
В нашем случае, b1 = -2/27 и q = 3, поэтому формула примет вид: bn = (-2/27) * 3^(n-1)
Теперь нам нужно найти восьмой член геометрической прогрессии (bn), поэтому положим n = 8 в формулу:
b8 = (-2/27) * 3^(8-1)
Для подсчета этого выражения, возьмем отдельные шаги:
8-1 = 7
3^7 = 2187 (чтобы вычислить это, продолжайте умножать 3 само на себя 7 раз, 3 * 3 * 3 * 3 * 3 * 3 * 3 = 2187)
Теперь продолжим вычисления:
b8 = (-2/27) * 2187
b8 = -4374/27
b8 = -162
Ответ: Восьмой член геометрической прогрессии равен -162.