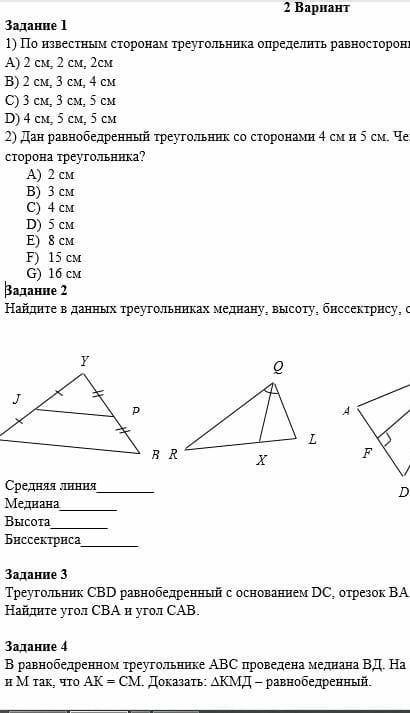
Найдите в данных треугольников медиану высоту биссектрису среднюю линию ​

Для начала разберемся, что такое медиана, высота, биссектриса и средняя линия треугольника.

Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. В данном треугольнике медиана можно наложить, соединив вершину A с серединой стороны BC и получив отрезок AD.

Высота - это отрезок, опущенный из вершины треугольника на противоположную сторону (или ее продолжение), перпендикулярно этой стороне. В данном треугольнике высоту можно наложить, опустив отрезок BE из вершины B на прямую AC.

Биссектриса - это отрезок, который делит угол треугольника на две равные части и соединяет вершину угла с серединой противоположной стороны. В данном треугольнике биссектрису можно наложить, соединив вершину C с серединой стороны AB и получив отрезок CF.

Средняя линия - это отрезок, который соединяет середины двух сторон треугольника. В данном треугольнике среднюю линию можно наложить, соединив середину стороны AC с серединой стороны AB и получив отрезок GM.

Теперь приступим к решению задачи.

1. Медиана:
- Находим середину стороны BC. Для этого можно сложить координаты точек B и C по каждой оси (x и y) и разделить результаты на 2.
SerBC = ( (xB + xC) / 2 , (yB + yC) / 2 )
- Соединяем вершину A с серединой стороны BC и получаем медиану AD.

2. Высота:
- Находим уравнение прямой, проходящей через вершину B и перпендикулярной стороне AC.
Уравнение перпендикулярной прямой: (x - xB) * (xB - xC) + (y - yB) * (yB - yC) = 0
Заменяем коэффициенты в уравнении на значения вершин A и C.
Уравнение прямой: (x - xB) * (xA - xC) + (y - yB) * (yA - yC) = 0
- Находим точку пересечения этой прямой с прямой AC. Для этого можно решить систему уравнений.
Уравнение прямой AC: (x - xA) * (xA - xC) + (y - yA) * (yA - yC) = 0
- Получаем точку пересечения E.
- Соединяем вершину B с точкой пересечения E и получаем высоту BE.

3. Биссектриса:
- Находим середину стороны AB. Для этого можно сложить координаты точек A и B по каждой оси (x и y) и разделить результаты на 2.
SerAB = ( (xA + xB) / 2 , (yA + yB) / 2 )
- Находим уравнение прямой, проходящей через вершину C и середину стороны AB.
Уравнение прямой: (x - xC) * (xC - xSerAB) + (y - yC) * (yC - ySerAB) = 0
- Соединяем вершину C с точкой пересечения F и получаем биссектрису CF.

4. Средняя линия:
- Находим середину стороны AC. Для этого можно сложить координаты точек A и C по каждой оси (x и y) и разделить результаты на 2.
SerAC = ( (xA + xC) / 2 , (yA + yC) / 2 )
- Находим середину стороны AB. Для этого можно сложить координаты точек A и B по каждой оси (x и y) и разделить результаты на 2.
SerAB = ( (xA + xB) / 2 , (yA + yB) / 2 )
- Соединяем точки SerAC и SerAB и получаем среднюю линию GM.

Таким образом, мы нашли медиану AD, высоту BE, биссектрису CF и среднюю линию GM для данного треугольника.