Найдите уравнения касательных к окружности x^2+y^2-2y=9, проходящих через точку М(7, 2). Можно с подробным решением

Ответы

HelpDZ1 02.09.2021 00:09

/////////////////////////////////////////////

Пошаговое объяснение:

Найдите уравнения касательных к окружности x^2+y^2-2y=9, проходящих через точку М(7, 2). Можно с под

ПОКАЗАТЬ ОТВЕТЫ

kobelevmiklip08h5g 02.09.2021 00:09

Приведу редко используемый в этой ситуации в надежде. что кто-нибудь другой даст и один из стандартных . $MN=\sqrt{(7-0)^2+(2-1)^2}=\sqrt{50}=5\sqrt{2}.$

Пусть K - точка касания одной из двух касательных с окружностью. Тогда KN=\sqrt{10} - ведь уравнение окружности x²+(y-1)^2=10, центр у нее в точке N(0;1), а радиус равен корню из 10.

Далее, поскольку касательная перпендикулярна радиусу, проведенному в точку касания, угол MKN прямой, KM²=50-10=40, а тангенс угла KMN равен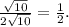 $\frac{\sqrt{10}}{2\sqrt{10}}=\frac{1}{2}.$

Поэтому. чтобы получить касательную, нужно прямую MN с угловым коэффициентом (то есть тангенсом угла наклона) 1/7 повернуть вокруг точки M на угол arctg(1/2) в ту или другую сторону. Поскольку

$tg(\alpha\pm\beta)=\frac{tg\alpha\pm tg \beta}{1\mp tg\alpha\cdot tg \beta},$ получаем угловые коэффициенты

$k_1=\frac{\frac{1}{7}+\frac{1}{2}}{1-\frac{1}{7}\cdot \frac{1}{2}}=\frac{9}{13};\ k_2=\frac{\frac{1}{7}-\frac{1}{2}}{1+\frac{1}{7}\cdot \frac{1}{2}}=-\frac{5}{15}=-\frac{1}{3}.$