Найдите уравнение касательной к графику функции у=х^2-2х+5 в точке пересечения его с осью координат
Другие вопросы по теме Математика
Популярные вопросы
- Боковая сторона разносторонней трапеции в которую вписан круг равна 12 см...
2 - ответьте на вопрос: Как отразилось пребывание Тютчева (22 года) за границей....
2 - Эссе на тему:Мне хотелось бы,чтобы моя родина была самой(нужно продолжить)...
3 - қария жаухардай үлкен мұздай кіші мұхит кит көл түлкі тау ит жұлдыз ыстық...
1 - начерти три перекасающися прямые. Сколько пересчения этих прямых может быть...
1 - Чому принц Джон налякався звістки, яка надійшла з Франції: а) організовувалась...
2 - Рассказ о случае который убедил вас в том что ваш друг настоящий...
1 - 3. Кратко расскажите про жизнь посадских и гостей. ...
1 - Геометрия 10 класс № 9.12 №15.2 №15.4...
3 - Мынау қалай шығад. Айтып жіберіңдерші...
2
Пошаговое объяснение:
Пусть мы верим тому, что уравнение касательной в точке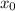 к графику функции
к графику функции 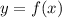 - это
- это 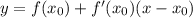
(Если надо вывести, напишите в комментариях)
Точка пересечения с осью ОРДИНАТ: (я вас правильно понял?)
В этой точке x = 0
Тогда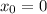 и
и 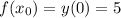
Найдём производную: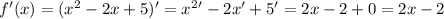
Найдём её значение в точке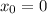 :
:
Запишем уравнение касательной:
ЕСЛИ ВАМ ЧТО-ТО НЕ ПОНЯТНО, НАПИГИТЕ МНЕ ОБ ЭТОМ В КОММЕНТАРИЯХ