Найдите угол между прямой, проходящей через точки A(-2; 1; 1) и B(0; 2; -1), и прямой, проходящей через точки C(1; 3; 0) и D(2; 1; 3). В ответ введите косинус этого угла, умноженный на 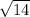
Другие вопросы по теме Математика
Популярные вопросы
- Спиши. вставь нужные предлоги. _нас большой красивый класс. _ на окнах...
3 - За 4 часа моторная лодка путь длиной 112 км за сколько часов она пройдет...
3 - Затранскрибировать предложение в маленькой деревеньке над небольшой речкой,...
1 - 20 1)страны африки расположены в бассейне рек нигер и замбези 2)страны...
1 - Вмагазине продали 654 кг муки манной крупы на 185 кг меньше а сахарного...
2 - Какая масса кальция потребуется для получения 3 моль оксида кальция...
1 - 6*6= 36 всё правильно а если 6: 6= 1 6+6+6+6+6+6=36...
3 - Сочинение на тему как надо защищать жабу...
1 - Как мы узнаем о жизни древних греков?...
3 - Диск электросчетчика сделала 30000 оборотов, что составило 24 киловатт...
3
Даны точки A(-2; 1; 1), B(0; 2; -1), C(1; 3; 0) и D(2; 1; 3).
Вектор АВ = (0-(-2); 2-1; -1-1) = (2; 1; -2), модуль равен √9 = 3.
Вектор CD = (2-1; 1-3; 3-0) = (1; -2; 3), модуль равен √14.
Косинус угла между ними равен:
cos (AB_CD) = (2*1+1*(-2)+(-2)*3)/(3√14) = -6/(3√14) = -2/√14 = -√14/7.
Угол между векторами — угол между направлениями этих векторов (наименьший угол). По определению, угол между двумя векторами находится в промежутке [0°; 180°].
То есть, угол может быть тупым при отрицательном косинусе его.
Угол равен arccos(-√14/7) = arccos(-0,534522484) = 2,134738968 радиан или 122,3115332 градуса.