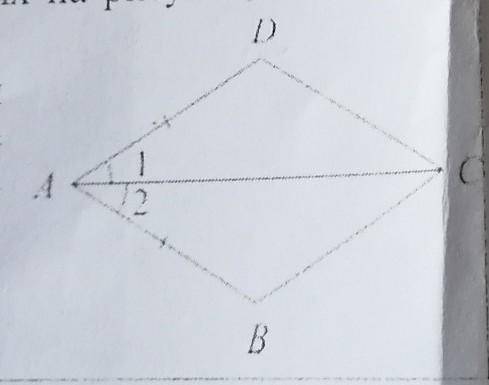
Найдите угол ACD, если ACB = 38° и длину стороны CD, если AB = 13см.
Другие вопросы по теме Математика
Популярные вопросы
- Решите уравнение , и уравнение с пропорциями 1. 3/14х-0.59=8/21х-1,24...
2 - Укажи предложение в котором две грамматические основы. 1)однажды...
2 - Диссоциации ba(hco3)2 соответствует уравнение ba(hco3)2 ba2+ +...
1 - Нужно с решением! из вершины b параллелограмма abcd проведены...
3 - Длина комнаты 7 м 50 см,а площадь 36...
3 - 1. решите уравнение 5у - 3,5 = 2у + 5,5...
2 - Периметр квадрата равен 97 дм 6 см . вычисли периметр равностороннего...
1 - Укажите глагол совершенного вида. а)строить б)выстраивать в)построить...
3 - 1,почему не с этими словами пишется раздельно не выкинешь, не...
2 - Как решать длинные уравнения с иксами...
2
CD=AB=13сантиметров
Дано: ACB = 38° и AB = 13 см.
Шаг 1: Найдем угол BAC.
Угол BAC является внешним по отношению к треугольнику BCD, а значит, его величина равна сумме вэленностей углов BCD и BDC.
Известно, что сумма углов треугольника равна 180°, поэтому BCD + BDC = 180° - BAC.
Заменяем известные значения: 38° + BDC = 180° - BAC.
Шаг 2: Найдем угол BDC.
Угол BDC является внутренним по отношению к треугольнику ABC, а значит, его величина равна 180° - ACB.
Заменяем известные значения: BDC = 180° - 38°.
Шаг 3: Найдем угол CBD.
Угол CBD и угол BAC являются вертикальными углами, поэтому их величина равна.
Заменяем известные значения: CBD = BAC.
Шаг 4: Найдем сторону CD.
Для нахождения стороны CD воспользуемся теоремой косинусов, которая гласит: c^2 = a^2 + b^2 - 2ab*cos(C), где c - длина стороны противолежащей углу C, a и b - длины двух других сторон и C - величина противолежащего угла.
Заменяем известные значения: CD^2 = AC^2 + AB^2 - 2 * AC * AB * cos(ACB).
Шаг 5: Решим уравнение и найдем длину стороны CD.
CD^2 = AC^2 + AB^2 - 2 * AC * AB * cos(ACB)
CD^2 = AC^2 + 13^2 - 2 * AC * 13 * cos(38°)
CD^2 = AC^2 + 169 - 26 * AC * cos(38°)
В данной задаче не указаны значения двух сторон треугольника ABC, а только угол ACB, поэтому без дополнительной информации мы не сможем точно определить длину стороны CD.
Надеюсь, эта информация поможет вам понять, как решить данную задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.
Это р/б треугольник A=C=70,B=40