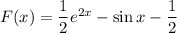Найдите ту первообразную функции f(x)=e²ˣ-cos x, график которой проходит через начало координат
Другие вопросы по теме Математика
Популярные вопросы
- черный цвет овса определяется доминантным геном a, а серый цвет...
3 - Округлите десятичные дроби ЗА ВЕРНЫЙ ОТВЕТ...
2 - Когда проходили Пунические войны?...
2 - ВСЕМИРНАЯ ИСТОРИЯ СОР ответьте на вопросы: 1) Объединение Германии...
2 - А)Екі мәтінге ортақ тақырыпты көрсетіңіз. а) Үйірін тапқан белтірік...
3 - Окей плз я не очень тороплюсь но иожно по быстрей и да я знаю что...
2 - https://67gymnasiumschool.sharepoint.com/:w:/r/sites/87222/DocLib/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D1%8F/02.03%20%D0%B1%D0%B6%D0%B1%20%D1%82%D0%B0%D0%BF%D1%81%D1%8B%D1%80%D0%BC%D0%B0%D1%81%D1%8B%20%20%20%20%20%20%20%D0%BE%D1%80%D1%8B%D0%BD%D0%B4%D0%B0%D1%83%20%D1%83%D0%B0%D2%9B%D1%8B%D1%82%D1%8B%2013/8%20%D1%81%D1%8B%D0%BD%D1%8B%D0%BF%20%D0%B1%D0%B6%D0%B1%203%20%D1%82%D0%BE%D0%BA%D1%81%D0%B0%D0%BD%20%D0%BA%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%20%D1%82%D0%BE%D1%80%20%D0%BA%D0%BE%D1%81%D1%82%D1%8B%D0%BC.docx?d=w120bc232bc174714a34f15b3cb81a009&csf=1&web=1...
2 - с сором по физике тока му**ки мимо...
2 - Дроби. Закрепление Сравни выражения.++–+НазадПроверить...
1 - Задания 1.Прочитайте тексты. Сформулируйте по каждому тексту 1...
3
Общий вид первообразных:
Подставим в уравнение:
ответ: