Найдите тангенс угла наклона к оси OX касательной графика функции
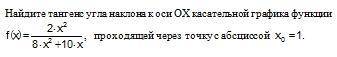
Другие вопросы по теме Математика
Популярные вопросы
- 3. Ученик написал копитал, помалчать, укланялись. Он утверждает, что...
3 - Вариант 5 1) Вычислить с пом. формул sin, cos и tg суммы и разности...
1 - . Сколько элементов включает в себя общественная система в соответствии...
2 - Анализ 1. Обълоните основную закономерность в распределении суммарноїй...
1 - «Компьютербасты жарты адамдар» өлеңінің тақырыбына эссе жазу....
1 - ответьте на вопрос: Мәтіннен есімдік бар сөйлемдерді,тауып көшіріп жазындар...
2 - Какой цифрой оканчивается 9 в 110 степени...
3 - Прочитай текст. Какой заголовок отражает основную мысль текста? Вывалилась...
2 - Өлеңдердің қайсысы атамекенге, туған жердің табиғатына сүйсінуден, қайсысы...
3 - Прочитай текст Ты никогда не задумывался о том, почему ты похож на папу...
1
Тангенс угла наклона к оси OX касательной графика функции равен производной функции в точке касания.
Дана функция у = 2х²/(8х² + 10х) = х²/(4х² + 5х).
Её производная равна:
y' = (2x*(4х² + 5х) - (8x + 5)*х²)/((4х² + 5х)²) = 5/(4х² + 5х)².
Находим y'(1) = 5/(4*1² + 5*1)² = 5/9² = 5/81.
ответ: тангенс равен 5/81.