Найдите радиус основания цилиндра наибольшего объема, который можно вписать в шар радиуса 6.
Другие вопросы по теме Математика
Популярные вопросы
- В-2 1. выберите правильный вариант ответа: если в первой части бессоюзного...
2 - На рисунке изображены животные сор хэлп...
2 - Опишите княжескую одежду с корзно в древней руси . только не надо много...
1 - Что происходило в 3 томе война и мир. кратко...
2 - Из деpевянного шаpа pадиуса r = 3 м тpебуется выpезать цилиндp наибольшего...
2 - Напишите эссе на тему если бы я был музыкантом...
1 - Графически обозначьте согласованые определения и расставьте недостающие...
1 - Сделать в си шарпв целочисленном массиве, сгенерированном случайным образом,...
3 - Дайте правильный ответ . 38 , по возможности сделайте на листочке если не...
2 - Спиши предложения, вставляя пропущенные буквы, расставляя недостающие знаки...
2
Пошаговое объяснение:
Рассмотрим осевое сечение. Пусть радиус окружности основания цилиндра равен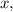 тогда
тогда 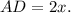 Из теоремы Пифагора для прямоугольного треугольника
Из теоремы Пифагора для прямоугольного треугольника 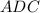
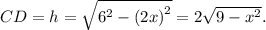
Объем цилиндра V = Sh = 2\pi {x^2}\sqrt {9 - {x^2}} .
Найдем производную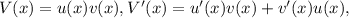 где
где 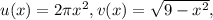
 — сложная функция:
— сложная функция:
Найдем максимум этой функции. Нули производной — числа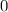 и
и 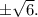 С метода интервалов видим, что функция возрастает от
С метода интервалов видим, что функция возрастает от 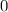 до
до 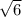 и убывает после
и убывает после 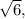 таким образом
таким образом 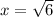 — точка ее максимума.
— точка ее максимума.