Найдите производную функции
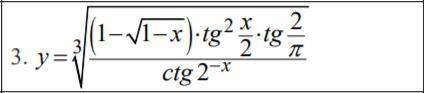
Другие вопросы по теме Математика
Популярные вопросы
- Середина К хорди АВ сполучена з центром О кола.Знайдіть кути трикутника ВОК ,якщо...
3 - Контрольна мовні аспекти вивченя реченнч...
2 - В четырехугольнике угол D на 32° меньше угла B. AB||CD; угл BCA=30°. Найдите...
2 - Найти стационарные точки, определить их тип и изобразить фазовые траектории для...
2 - Позначте рядок у якому частку треба писати ререз дефіс А)а(як)же Б)Ану(ж)бо В)все(ж)таки...
2 - Укажите типы односоставных предложений в каждом пункте (переписывать предложения...
3 - Складнопідрядним реченням з неоднорідною підрядністю є речення А Це буде там,...
3 - Основа рівнобедренного трикутника дорівнює 12, а висота, що проведена до основи...
1 - Задача 4: Американские горки Аттракцион «Американские горки» представляет собой...
3 - Які реагенти потрібно використати для добування натрій гідроксиду? * а) Na2SO4...
3
Остаётся только подставить значения вместо переменных в последней формуле, и ответ готов, для вычисления использовались функции дифференцирования