Найдите площадь прямоугольного треугольника если гипотенуза равна 13,а один из острых углов равен 45 градусов

Раз один угол 45°, то второй угол: 90° - 45° = 45°, следовательно, треугольник является равнобедренным прямоугольным треугольником, катеты у него равны.

с - гипотенуза

а - катеты

a = c/√2 = 13/√2

Площадь треугольника: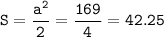 кв. ед.

Сумма острых углов прямоугольного треугольника равна 90°. Т.к. один из острых углов равен 45°, то и второй угол равен 45°. Значит, данный треугольник еще и равнобедренный, т.е. его катеты равны.

Пусть катеты равны х, тогда по теореме Пифагора получим х² + х² = 13²,

2х² = 169, х² = 169/2.

Площадь прямоугольного треугольника равна половине произведения его катетов, т.е. S = 1/2 · х · х = 1/2 · х² = 1/2 · 169/2 = 169/4 = 42, 25.

ответ: 42,25.