Найдите площадь поверхности правильной четырехугольной пирамиды высота которой равна 8см и угол между высотой и апофемой 45°
Ответы
Раз угол между высотой и апофемой равен 45°, то треугольник, образованный высотой, апофемой и соединением высоты и апофемы через основание пирамиды, то этот треугольник — равнобедренный, а значит его катеты равны, при этом у нас один известен и он равен 8. Тогда апофема равна 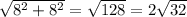 , а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна
, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 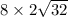 , а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна
, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 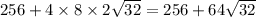 Будем надеяться, что я не ошибся в вычислениях.
Будем надеяться, что я не ошибся в вычислениях.
ПОКАЗАТЬ ОТВЕТЫ
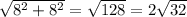 , а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна
, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 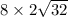 , а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна
, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 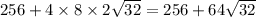 Будем надеяться, что я не ошибся в вычислениях.
Будем надеяться, что я не ошибся в вычислениях.
Другие вопросы по теме Математика
Популярные вопросы
- 1)чему учит сказка теплый 2)пословицу к этой сказке...
1 - Впиши пропущенные разрядные слагаемые 875007=800000+ 5000+ 384070= + +4000+...
1 - Какой радиус должна иметь окружность с центром в точке p(-3; 6),чтобы...
1 - X^{2} +(х-2)^{2} как раскрыть скобки...
3 - Укажи трёхсложное слово а) портрет в) шагаю б) мир г) аквариум...
1 - На какие вопросы отвечают слова что? , шторы, стул, доска, окно, парта,...
3 - Один ученик может убрать класс за 20 мин, а другой за 30 мин. за сколько...
1 - Решите катер проплыл по течению реки за 2,4 ч расснояние 55 целых 1/ 5...
1 - Разобрать слова по составу горных, растоплят, шлифует, перекатывает...
2 - Придумай предложения со словами поставить и расставить...
3