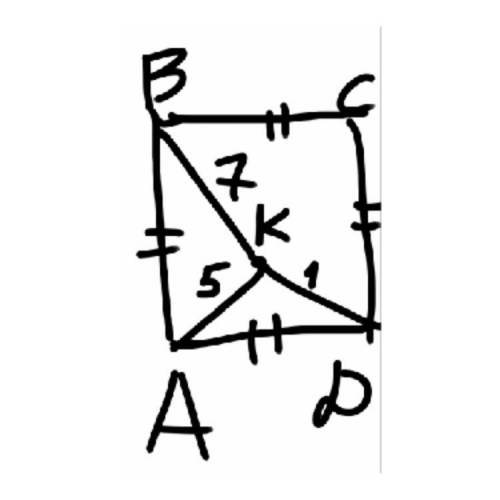
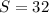Найдите площадь квадрата ABCD
Другие вопросы по теме Математика
Популярные вопросы
- Номер 1: решите неравенство -7х+1 -1 номер 2: решите уравнение (х+10)...
1 - Среди зверюшек,. среди какая часть речи?...
3 - Решить) древний учебник) две лампы в 100кд и 50кд находятся на расстоянии...
2 - Собственная скорость моторной лодки 6,7 км\ч,скорость течения реки...
2 - Напишите сочинение рассуждение на тему хорошо учиться - это значит.....
1 - 2∙а + 1,5∙с, если а=1,4 и с=0,8 найдите значение выражения...
2 - Определить тип односоставного предложения. 1) будешь играть с нами?...
3 - Правописание суффиксов чик щик ек ик...
1 - Составить текст из 10 предложений на тему мой выходной, с глаголами...
1 - Sin^альфа +cos^альфа если sin альфа +cos альфа =1,4...
3
ответ: 32
Пошаговое объяснение:
Смотрите рисунок.
Пусть сторона квадрата равна , тогда площадь квадрата
, тогда площадь квадрата
По теореме косинусов, учитывая, что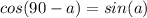 имеем:
имеем:
Поскольку угол - острый, должно быть выполнено неравенство:
- острый, должно быть выполнено неравенство:
Преобразуем:
Сложим оба уравнения, учитывая основное тригонометрическое тождество: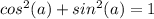
Таким образом :