Найдите площадь фигуры ограниченной графиками функций: 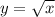
, y=2-x, y=0, через интегрирование
Другие вопросы по теме Математика
Популярные вопросы
- Наиболее энергично взаимодействуют с водой 1) калий 2) магний 3) стронций...
2 - Укажите какие-нибудь десять делителей произведения 32*24*21 5 класс...
1 - Вставити, де треба, пропущені букви д…кан, ауд…торія, гру…а, і…унологія,...
3 - Уаня раскрасила 5 цветков а тания на два больше скл цветов раскрас аня...
2 - Вчем особенности реакций полимеризации у диеновых углеводородов с сопряженными...
3 - Кто нибудь, разобраться! - амфотерные соединения, например реакция sno+ 2naoh...
1 - Чему равно значение выражения (3/7+ 1/9) × 63...
1 - Простое вещество с наиболее ярко выраженными металлическими свойствами 1)...
3 - На лесничем складе один штабель состоит из досок длинной 4 м, толщиной 5...
3 - :у прямоугольника длина 5 см, а ширина 2 см. какова площадь и периметр прямоугольника...
1
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую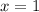 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
(см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
А теперь складываем и находим искомую площадь.
ответ: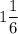 .
.