Популярные вопросы
- Вслучайном эксперименте симметричную монету бросают дважды .найдите...
1 - Чем объясняется различие в солености вод и красного морей?...
1 - Почему в одной части страны идет дождь. а в другой нет.. почему.....
3 - Дано: ag2s hbr ca al2o3 добути: 6 сложных и 4 простых...
3 - Написать призентацию тема люди в тундри...
3 - Кто-нибудь , ! 1) на прямой проводник длиной l=0,5 м, расположенный...
2 - Дайте полное решение** предложите не менее трех получения сульфата...
1 - ответить на два вопроса 1) происхождение растений 2) этапы развития...
1 - Мне нужно сачыненне на тему чалавек за усе адказны на зямли...
3 - Втреугольник с двумя углами a и b вписана окружность. найдите...
3
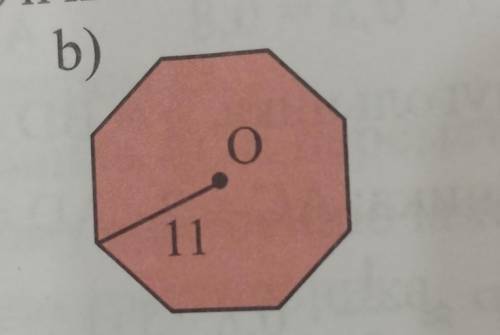
Количество сторон правильного многоугольника n=8; радиус описанной около него окружности R=11;
Периметр найдем по формуле Р=2*R*sin(180°/n)=2*11*sin22.5°=
22*√((1-сos45°)/2)=22*√((1-√2/2)/2)=22*√((2-√2)/4)=22*(2-√2)/2=11*(2-√2)
радиусы соединим с вершинами, получим восемь равнобедренных треугольников, с боковой стороной 11, и углом при вершине 360°/8=45°, увеличив площадь одного такого треугольника в 8 раз, найдем площадь правильного восьмиугольника
8*(11*11*sin45°)/2=4*121*√2/2==242√2 (ед. кв.)