Найдите область определения функции 1) y=2x-1/3
2) y=5/x-5
3) y=x-3/(x+3)(2-x)
4) y=√2x^2-5x+2
5) y= √2x+1/x+3​

1) D = R. 2) D = (-∞; 5) U (5; +∞). 3) D = (-∞; -3) U (-3; 2) U (2; +∞). 4) D = (-∞;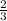 ) U ( 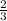; +∞). 5) D = (-∞; -3) U (-3; +∞).

Пошаговое объяснение:

Как мы знаем, D = множество аргументов, при котором уравнение имеет смысл.

1) y =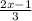 , и здесь будет D = R (любое число), т.к. делитель всегда будет 3.

2) y = ,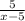

х - 5 ≠ 0;

x ≠ 5.

D = (-∞; 5) U (5; +∞).

3) y = ,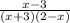

1. х + 3 ≠ 0

2. х ≠ -3.

1. 2 - х ≠ 0.

- х ≠ -2.

х ≠ 2.

D = (-∞; -3) U (-3; 2) U (2; +∞).

4) Корень ликвидируется, т.к. есть степень.

2х-5х+2 ≠ 0.

-3х + 2 ≠ 0.

-3х ≠ -2.

3х ≠ 2.

х ≠ .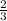

D = (-∞;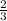 ) U ( ; +∞).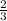

5)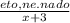 , х + 3 ≠ 0.

х ≠ -3.

D = (-∞; -3) U (-3; +∞).