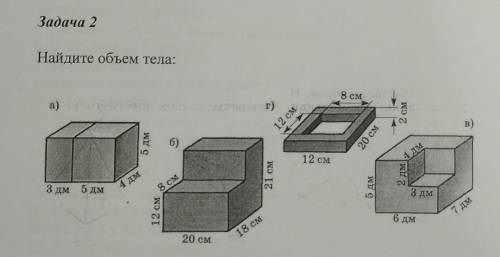
Найдите объем тела.

а)
б)
в)
г)​

г по-моему точно не знаю

Чтобы найти объем каждого из тел, мы будем использовать формулу для нахождения объема пространственной фигуры, соответствующей каждому варианту.

а) На рисунке "а" изображен прямоугольный параллелепипед. Формула для нахождения объема такого тела: объем = длина x ширина x высота. На рисунке видно, что длина составляет 6 единиц, ширина равна 4 единицам, а высота тела составляет 3 единицы. Подставим данные в формулу: объем = 6 x 4 x 3 = 72 единицы объема.

б) На рисунке "б" изображена цилиндрическая банка. Формула для нахождения объема цилиндра: объем = площадь основания x высота. При этом площадь основания цилиндра равна площади круга, которая находится по формуле: площадь = пи x радиус^2. На рисунке видим, что радиус круга равен 2 единицам, а высота банки составляет 8 единиц. Подставим данные в формулы: площадь = пи x 2^2 = 4пи (единицы площади), объем = 4пи x 8 = 32пи единиц объема. В данном случае, ответ будет в виде числа пи, так как задан радиус, но нет конкретного его значения.

в) На рисунке "в" изображен конус. Формула для нахождения объема конуса: объем = площадь основания x высота / 3. Как и в случае с цилиндром, площадь основания конуса находится по формуле площади круга, а высота тела изображена на рисунке. В данном случае радиус круга равен 3 единицам, а высота составляет 6 единиц. Подставим данные в формулы: площадь = пи x 3^2 = 9пи (единицы площади), объем = 9пи x 6 / 3 = 18пи единиц объема.

г) На рисунке "г" изображена пирамида. Формула для нахождения объема пирамиды: объем = площадь основания x высота / 3. Подставим известные значения: площадь основания пирамиды находится по формуле площади прямоугольника (продолжение см. а), ширина равна 4 единицам, а длина - 3 единицам), и равна 4 x 3 = 12 единицам площади. Высота пирамиды указана на рисунке и составляет 5 единиц. Подставим данные в формулы: объем = 12 x 5 / 3 = 20 единиц объема.

Итак, ответы на вопросы:

а) Объем тела равен 72 единицам объема.
б) Объем тела равен 32пи единицам объема.
в) Объем тела равен 18пи единицам объема.
г) Объем тела равен 20 единицам объема.