1. Математика
  2. Найдите натуральное число

Найдите натуральное число при делении которого на 1 5\13,1 7\9 и 2,4 получается натуральное число

Mariaaglotkova Mariaaglotkova    3   31.03.2019 11:50    0

Ответы
тагієва тагієва  27.05.2020 22:08

Требуется найти натуральное число, которое бы делении на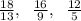 \frac{18}{13}, \;\; \frac{16}{9}, \;\; \frac{12}{5} давало бы натуральное число.

 

Поскольку вопрос о наименьшем решении не стоит, то перемножив числители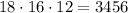 18 \cdot 16 \cdot 12 = 3456, получим натуральное число, нацело делящееся на указанные числа.

 

Если нужно именно наименьшее натуральное, делящееся на 18, 16 и 12 (и, соответственно, на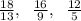 \frac{18}{13}, \;\; \frac{16}{9}, \;\; \frac{12}{5} ), то ищем наименьшее общее кратное этих чисел.

 

Раскладываем 18, 16 и 12 на простые множители, группируя по множителям в такой-то степени:

 

18 = 3 \cdot 3 \cdot 2 = 3^2 \cdot 2^1

16 = 2 \cdot 2 \cdot 2 \cdot 2 = 2^4

12 = 3 \cdot 2 \cdot 2 = 3^1 \cdot 2^2

 

Наименьшим общим кратным будет произведение наибольших степеней каждого из простых делителей, в нашем случае:

 

n = 3^2 \cdot 2^4 = 144

 

Это и будет наименьшим из искомых натуральных чисел.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
alekseywindas alekseywindas  08.02.2021 14:04
пож вычислить интеграл ∫ x^2 √(1+3x^3 ) dx...
царапина123 царапина123  08.02.2021 14:04
Под какой цифрой нужно записать цифру 8 при сложении чисел: 14,573 + 2,81​...
tolkov05 tolkov05  08.02.2021 14:03
За отчетный квартал фирмой по производству одежды изготовлено и реализовано 320 курток по цене 1150 руб. и 415 платьев по цене 890 руб. (цены предприятия). Затраты на...
kuchatrupov47 kuchatrupov47  08.02.2021 14:03
34.2. 1) 27 - a ; 5) 0,008 + a ;2) b3 + 125;6) 0,216 – 63;3) 64 - m;7) 0,027 + n°;4) 8+ 9%;8) 0,125 – m.​...
валя357 валя357  08.02.2021 14:03
Если задуманное двузначное число сложить с суммой его цифр, то получится 2424. Если же из задуманного двузначного числа вычесть 99, то получится двузначное число, записанное...
Rollov35 Rollov35  08.02.2021 14:03
Семь целых-три восьмых решить ​...
bayan6 bayan6  08.02.2021 14:03
Джээнбек и Ира затратил на выполнение домашниго задания 2 часа 24 минуты , при этом Ира затратила на 30 минут меньше. Сколько времени затратил каждый? Помагите очень...
Sabinafei Sabinafei  08.02.2021 14:03
D+c×3 d- ( c - 369) d× 3+ c× 2​...
саня1361 саня1361  08.02.2021 14:03
4.35. Известно, что a |B| lc|. Как могут быть расположены на числовой прямой числа а, b и c. Перечислите все возможные случаи. Схематично изобразите все случаи на числовой...
yastremskayaal yastremskayaal  08.02.2021 14:03
Составь задачу и реши её по чертежу....

Популярные вопросы